Question

How do you find the value of \[\sin \dfrac{\pi }{6}\]?

Answer 1

Hint: To solve this trigonometry problem, we will take the help of a right-angled triangle. With the triangle we will mark a \[\vartriangle ABC\] such that it is a \[{30^ \circ } - {60^ \circ } - {90^ \circ }\]. In that we will take the measure of the hypotenuse as a. Then according to that we will mark the sides opposite to remaining angles. Then from that we will use the ratio of sin function to get the necessary value.

Complete step-by-step answer:
Let’s draw the necessary diagrams first.

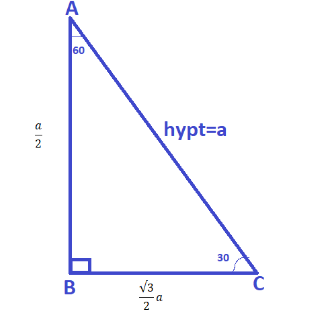
Now we can observe the diagram above very carefully.
We know that the side opposite to a right angle is known as hypotenuse. So we have assigned the value of hypotenuse as a.
\[
  \angle A = {60^ \circ } \\
  \angle B = {90^ \circ } \\
  \angle C = {30^ \circ } \;
\]
Now we know that,
\[\dfrac{\pi }{6} = {30^ \circ }\]
Then,
\[\sin \dfrac{\pi }{6} = \sin {30^ \circ } = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}\]
Now the side opposite to \[{30^ \circ }\] is half of the hypotenuse as shown in the diagram above.
So, assigning the values in the equation above we get,
 \[\sin \dfrac{\pi }{6} = \dfrac{{\dfrac{a}{2}}}{a}\]
On solving we get,
\[\sin \dfrac{\pi }{6} = \dfrac{a}{{2a}}\]
Cancelling the a term we get,
\[\sin \dfrac{\pi }{6} = \dfrac{1}{2}\]
This is the required answer.
So, the correct answer is “$\dfrac{1}{2}$”.

Note: Here we have to note that finding this type of values is the very basic of trigonometry. So when we need to find the functions like sin, cos, tan and the three remaining functions we will use this method only. For cos function the ratio is of adjacent side to hypotenuse. And in tan function it is the ratio of opposite side to adjacent side of the asked angle.
Also note that a right angle triangle can be of \[{45^ \circ } - {45^ \circ } - {90^ \circ }\] but in this case we need the triangle so used because the value of sin function asked is not \[{45^ \circ } - {45^ \circ } - {90^ \circ }\].