Question

Find the value of $\sin \,{{1845}^{{}^\circ }}$

Answer 1

Hint: Convert the given angle in the expression of the problem to acute angle form i.e. between ${{0}^{{}^\circ \,}}-\,{{90}^{{}^\circ }}\left( \,\dfrac{\pi }{2}\, \right)$. And use the quadrant rules that sin function is positive in the first and second quadrant and negative in the third and fourth quadrant. If the angle in function has involvement of multiple of $\dfrac{\pi }{2}\left( \text{not}\,\pi \right)$ i.e., of type $\dfrac{n\pi }{2}\pm \theta $, then change sine function to cosine or if summation of angle is of type $n\pi \pm \theta $, then do not change the trigonometric function. Use the above rules to get the answer. Use: $\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$.

Complete step-by-step answer:

Given expression in the problem is $\sin \,{{1845}^{{}^\circ }}$.

Let us suppose the value of the given expression is P so, we can write the equation as,
$P=\sin \,{{1845}^{{}^\circ }}..............(i)$

Now, we can observe that the angle involved in the above expression is not lying in ${{0}^{{}^\circ }}-\,{{90}^{{}^\circ }}$ i.e., not acute angle and we have known values of trigonometric function only in ${{0}^{{}^\circ }}\,-{{90}^{{}^\circ }}$. It means we have to convert the given angle to an acute angle form with the help of some trigonometric identities.
Hence, let us divide the given expression by ${{180}^{{}^\circ }}$, so, that we can write the given angle in form of a sum of angle which is multiple of ${{180}^{{}^\circ }}$ in the following way:

\[{{1845}^{{}^\circ }}={{180}^{{}^\circ }}\times 10+{{45}^{{}^\circ }}..............(ii)\]

Now, as we know the radian representation of ${{180}^{{}^\circ }}$ is given as \[\pi \text{ radian}={{180}^{{}^\circ }}................(iii)\]

Now, we can write ${{45}^{{}^\circ }}$ by the above relation as

$\begin{align}

  & {{180}^{{}^\circ }}=\pi \text{ radian} \\

 & \Rightarrow {{45}^{{}^\circ }}=\dfrac{\pi }{{{180}^{{}^\circ }}}\times {{45}^{{}^\circ }} \\

 & \Rightarrow {{45}^{{}^\circ }}=\dfrac{\pi }{4}\text{radian}...............(iv) \\

 & \\

\end{align}$

Now, we can put ${{1845}^{{}^\circ }}$ as $10\pi +\dfrac{\pi }{4}\,$ in the given expression in the problem i.e., in equation (i). So, we can re-write the equation (i) as
$P=\sin \left( 10\pi +\dfrac{\pi }{4} \right)..................(v)$

Now, as we know the quadrant angles are defined as

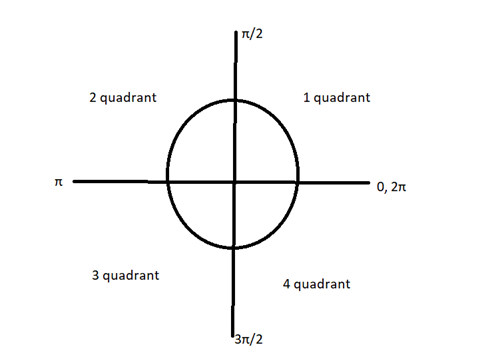
Now, we can apply the trigonometric rules for the conversion of trigonometric expressions by changing its angle.

Now, we can observe the equation (v) and get the angle involved with the trigonometric expression i.e., $10\pi +\dfrac{\pi }{4}$. We lie in 1st quadrant because $10\pi $ is a multiple of $2\pi $ and as $2\pi $ lies at the same position where 0 lies, it means $10\pi $ is multiple of $2\pi $ and if we, rotate 5 times around the origin then $10\pi $ will lie at same position where o lies \[\left( 10\pi =5\times 2\pi \right)\] and we are adding $\dfrac{\pi }{4}$ to $10\pi $ it means the angle $10\pi +\dfrac{\pi }{4}$ will lie in 1st quadrant as well.

Now, as $10\pi +\dfrac{\pi }{4}$ is expressed in sum $10\pi $, which is multiple of$\pi $; so, as per the trigonometry rules, the trigonometry function will not change with the expression which is involved a sum of angles which is multiple of $\pi $. It means, we can give some identities related to sin function and angle lying in 1st quadrant as

$\begin{align}

  & \sin \left( 2\pi +\theta \right)=\sin \theta \\

 & \sin \left( 4\pi +\theta \right)=\sin \theta \\

 & . \\

 & . \\

 & . \\

 & \sin \left( n\pi +\theta \right)=\sin \theta \\

\end{align}$

Where n is an even integer.

 So, using the above expression, we get equation (v) as: -

$P=\sin \left( 10\pi +\dfrac{\pi }{4} \right)=\sin \dfrac{\pi }{4}$

Now, we know that the value of $\sin \dfrac{\pi }{4}$ is $\dfrac{1}{\sqrt{2}}$. Hence, value of P is given as,

$P=\dfrac{1}{\sqrt{2}}$

So, we get the value of $\sin \,{{1845}^{{}^\circ }}$ as

$\sin \left( {{1845}^{{}^\circ }} \right)=\dfrac{1}{\sqrt{2}}$

Hence, $\dfrac{1}{\sqrt{2}}$ is the answer of the problem.


Note: We need to know two important rules involved in the conversion of
trigonometric function with respect to the angles.

Take care of signs with the help of given trigonometric function and the quadrant in which the angle is lying. This rule can be given as

if the angle involved inside the trigonometric function is multiple of $\dfrac{\pi }{2}$ (not multiple of $\pi $). i.e., $\dfrac{n\pi }{2}\pm \theta $, where n is an odd integer, then we need to convert the

$\begin{align}

  & \sin \rightleftarrows \cos \\

 & \tan \rightleftarrows \cot \\

 & \sec \rightleftarrows \csc \\

\end{align}$

If the angle involve in sum is multiple of $\pi $ i.e.$\dfrac{n\pi }{2}\pm \theta $ type, then trigonometric function will remain same.

Use the above two rules for the conversion of any trigonometric function by changing their angles.