Question

Find the value of \[\left( {\dfrac{1}{{\cos C}}} \right)\]?

Answer 1

Hint: Here the question is related to trigonometry, we have to find the value of the given trigonometric function. This can be found, by using the standard trigonometric definition and by the reciprocal trigonometric functions we get the required value.

Complete step by step solution:

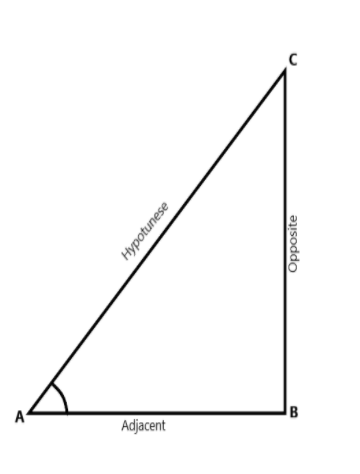
Trigonometric ratios: Some ratios of the sides of a right-angle triangle with respect to its acute angle called trigonometric ratios of the angle.
Let us consider the triangle ABC where angle \[CAB\] is an acute angle. BC is the opposite to the angle A and AB is the adjacent to the angle A. So, we call BC as opposite side and AB is adjacent side and AC is hypotenuse.
The trigonometric ratios of angle A in the given right angled triangle are defined as.
Sine of \[A = \dfrac{{Opposite\,side\,of\,A}}{{hypotenuse}} = \dfrac{{BC}}{{AC}}\]
Cosine of \[A = \dfrac{{Adjacent\,side\,of\,A}}{{hypotenuse}} = \dfrac{{AB}}{{AC}}\]
Tangent of \[A = \dfrac{{Opposite\,side\,of\,A}}{{Adjacent\,side\,of\,A}} = \dfrac{{BC}}{{AB}}\]
Cosecant of \[A = \dfrac{{hypotenuse}}{{Opposite\,side\,of\,A}} = \dfrac{{AC}}{{BC}}\]
Secant of \[A = \dfrac{{hypotenuse}}{{Adjacent\,side\,of\,A}} = \dfrac{{AC}}{{AB}}\]
Cotangent of \[A = \dfrac{{Adjacent\,side\,of\,A}}{{Opposite\,\,side\,of\,A}} = \dfrac{{AB}}{{BC}}\]
The ratios defined are abbreviated as sin A, cos A, tan A, csc A or cosec A, sec A and cot A
These functions are defined as the reciprocal of the standard trigonometric functions: sine, cosine, and tangent, and hence they are called the reciprocal trigonometric functions.
The reciprocal trigonometric functions are: \[\dfrac{1}{{\sin A}} = \cos ec\,A\], \[\dfrac{1}{{\cos A}} = sec\,A\] and \[\dfrac{1}{{\tan A}} = \cot \,A\].
Consider the given question:
We have to find the value of \[\left( {\dfrac{1}{{\cos C}}} \right)\]
By using a Reciprocal trigonometric function
\[ \Rightarrow \,\,\dfrac{1}{{\cos C}} = sec\,C\]
Hence, the value of \[\dfrac{1}{{\cos C}} = sec\,C\].
So, the correct answer is “\[\dfrac{1}{{\cos C}} = sec\,C\]”.

Note: The trigonometry ratios are sine, cosine, tangent, cosecant, secant and cotangent. These are abbreviated as sin, cos, tan, csc, sec and cot. We must know about the trigonometry definitions, identities and formulas which are involving the trigonometry ratios, while solving the trigonometry based questions.