Question

How do you find the value of k so that $\left( -2,1 \right)$ satisfies $kx+6y=k$?

Answer 1

Hint: We are given that $\left( -2,1 \right)$ satisfies $kx+6y=k$. A point satisfies an equation of line it is on the line itself. Therefore, we put the values of $x=-2,y=1$ in $kx+6y=k$. We get a linear equation of k. we solve the equation to get the value for k.

Complete step-by-step solution:
We have to find the value of k where the point $\left( -2,1 \right)$ satisfies $kx+6y=k$.
The point will satisfy the equation when we put the point in the equation.
So, we put $x=-2,y=1$ in the equation of $kx+6y=k$.
We get $k\times \left( -2 \right)+6\times 1=k$. Simplifying we get $-2k+6=k$.
Now we have to find the solution of the k from the equation of $-2k+6=k$.
All the terms in the equation of $-2k+6-k=0$ are either variable of $k$ or a constant. We first separate the variables and the constants.
We take the variables to get $-2k-k$.
The binary operation of subtraction gives $-2k-k=-3k$.
There is one constant which is 6.
The binary operation of addition gives us $-3k+6=0$ which gives $3k=6$.
Now we divide both sides of the equation with 3 to get
\[\begin{align}
  & 3k=6 \\
 & \Rightarrow \dfrac{3k}{3}=\dfrac{6}{3} \\
 & \Rightarrow k=2 \\
\end{align}\]
Therefore, the final solution becomes \[k=2\].

Note: Putting the value of \[k=2\], we get the line as $2x+6y=2$. Its simplified form is $x+3y=1$. We try to draw the line in the graph and get

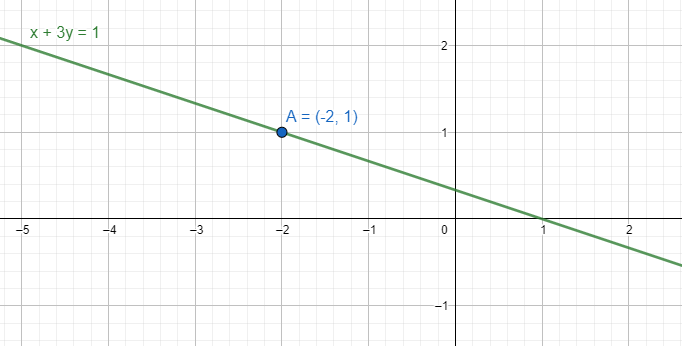
We can see that the point $\left( -2,1 \right)$ is on the line of $x+3y=1$.