Question

Find the value of $ \dfrac{4\sin 65{}^\circ }{5\cos 25{}^\circ }-\dfrac{13\cos 53{}^\circ \cos ec37{}^\circ }{5\left( {{\sec }^{2}}32{}^\circ -{{\cot }^{2}}58{}^\circ \right)} $ .

Answer 1

Hint: Start by using the relation between the complementary ratios like $ \sin \left( 90{}^\circ -x \right)=\cos x $ , $ \cos ec\left( 90{}^\circ -x \right)=\sec x $ and $ \cot \left( 90{}^\circ -x \right)=\tan x $ to convert the terms in the expression to suitable forms. Then use the formula $ {{\sec }^{2}}x-{{\tan }^{2}}x=1\text{ and secx}\text{.cosx=1} $ to eliminate all trigonometric terms. Finally, solve the expression to reach the answer.

Complete step-by-step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

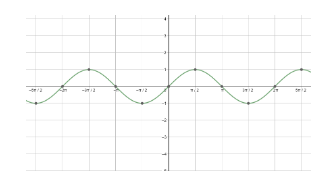
Next, let us see the graph of cosx.

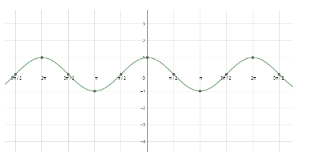
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $ 2{{\pi }^{c}} $ . So, we can say that the fundamental period of the cosine function and the sine function is $ 2{{\pi }^{c}}=360{}^\circ $ . So, we can mathematically show it as:
 $ \sin (2{{\pi }^{c}}+x)=\sin (360{}^\circ +x)=\sin x $
 $ \cos (2{{\pi }^{c}}+x)=cos(360{}^\circ +x)=\cos x $
Also, some other results to remember are:
\[\sin \left( \dfrac{{{\pi }^{c}}}{2}-x \right)=\sin (90{}^\circ -x)=\cos x\]
\[\cos \left( \dfrac{{{\pi }^{c}}}{2}-x \right)=\cos (90{}^\circ -x)=\sin x\]
 $ \cos ec\left( 90{}^\circ -x \right)=\sec x $
 $ \cot \left( 90{}^\circ -x \right)=\tan x $
We will now solve the equation given in the question.
 $ \dfrac{4\sin 65{}^\circ }{5\cos 25{}^\circ }-\dfrac{13\cos 53{}^\circ \cos ec37{}^\circ }{5\left( {{\sec }^{2}}32{}^\circ -{{\cot }^{2}}58{}^\circ \right)} $
 $ =\dfrac{4\sin \left( 90{}^\circ -25{}^\circ \right)}{5\cos 25{}^\circ }-\dfrac{13\cos 53{}^\circ \cos ec\left( 90{}^\circ -53{}^\circ \right)}{5\left( {{\sec }^{2}}32{}^\circ -{{\cot }^{2}}\left( 90{}^\circ -32{}^\circ \right) \right)} $
We know \[\sin \left( \dfrac{{{\pi }^{c}}}{2}-x \right)=\sin (90{}^\circ -x)=\cos x\] , so, our equation becomes:
 $ =\dfrac{4\cos 25{}^\circ }{5\cos 25{}^\circ }-\dfrac{13\cos 53{}^\circ \cos ec\left( 90{}^\circ -53{}^\circ \right)}{5\left( {{\sec }^{2}}32{}^\circ -{{\cot }^{2}}\left( 90{}^\circ -32{}^\circ \right) \right)} $
 $ =\dfrac{4}{5}-\dfrac{13\cos 53{}^\circ \cos ec\left( 90{}^\circ -53{}^\circ \right)}{5\left( {{\sec }^{2}}32{}^\circ -{{\cot }^{2}}\left( 90{}^\circ -32{}^\circ \right) \right)} $
We also know $ \cos ec\left( 90{}^\circ -x \right)=\sec x $ and $ \cot \left( 90{}^\circ -x \right)=\tan x $ . So, if we use this in our equation, we get
 $ =\dfrac{4}{5}-\dfrac{13\cos 53{}^\circ sec53{}^\circ }{5\left( {{\sec }^{2}}32{}^\circ -{{\tan }^{2}}32{}^\circ \right)} $
Now, we will use the identities $ {{\sec }^{2}}x-{{\tan }^{2}}x=1\text{ and secx}\text{.cosx=1} $ . On doing so, we get
 $ =\dfrac{4}{5}-\dfrac{13\times 1}{5\times 1}=\dfrac{4}{5}-\dfrac{13}{5}=-\dfrac{9}{5} $
Therefore, the answer to the above question is $ -\dfrac{9}{5} $ .

Note: Be careful that you don’t miss the negative sign in the final answer, as it is general observation that students solve the expressions correctly but misses the negative sign in the last step leading to the wrong answer. Also, remember the property of complementary angles of trigonometric ratios.