Question

How do you find the value of $\cot 60^\circ $?

Answer 1

Hint: Here we can proceed by finding the $\sin {\text{ and cos}}$ of the same angle as given and we know that $\tan x = \dfrac{{\sin x}}{{\cos x}}$ and therefore we can divide both the values of the $\sin {\text{ and cos}}$ of the same angle and get the exact value of the $\cot 60^\circ $.

Complete step by step solution:
Now we are given to find the exact value of $\cot 60^\circ $
We know that:
$\sin \left( {60^\circ } \right) = \dfrac{{\sqrt 3 }}{2}$$ - - - - (1)$
$\cos \left( {60^\circ } \right) = \dfrac{1}{2} - - - - (2)$
Now we can find the relation between $\sin ,\cos ,\tan $ to get the value of the $\cot \left( {60^\circ } \right)$
Let us consider the triangle $ABC$ right-angled at $B$

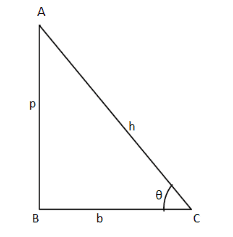
We know that:
$\sin \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}} - - - - (3)$
$\cos \theta = \dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}} - - - - (4)$
We also know that:
$\cot \theta = \dfrac{{{\text{base}}}}{{{\text{perpendicular}}}} - - - - (5)$
Now if we divide the equation (3) and (4) we will get:
$\dfrac{{\cos \theta }}{{\sin \theta }} = \dfrac{{\dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}}}}{{\dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}}}} = \dfrac{{{\text{base}}}}{{{\text{perpendicular}}}}$
Hence we get that:
$\dfrac{{\cos \theta }}{{\sin \theta }} = \dfrac{{{\text{base}}}}{{{\text{perpendicular}}}} - - - - (6)$
Now we can compare the equation (5) and (6) to get the required relation between $\sin ,\cos {\text{ and tan}}$
On comparing both equation (5) and (6) we can say that:
$\cot \theta = $$\dfrac{{\cos \theta }}{{\sin \theta }}$
So we know the value of $\sin \left( {60^\circ } \right) = \dfrac{{\sqrt 3 }}{2}$ and $\cos \left( {60^\circ } \right) = \dfrac{1}{2}$
Now we know that:
$\cot \theta = $$\dfrac{{\cos \theta }}{{\sin \theta }}$
Here putting the value of $\theta = 60^\circ $ we get:
$\cot 60^\circ = $$\dfrac{{\cos 60^\circ }}{{\sin 60^\circ }}$$ = \dfrac{{\dfrac{1}{2}}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{\left( 1 \right)(2)}}{{(\sqrt 3 )(2)}} = \dfrac{1}{{\sqrt 3 }}$
Hence by this method we have got the exact value of the given trigonometric function which is $\cot 60^\circ $
So in order to calculate cotangent of any angle we need to just divide the cosine and sine of the same angle and we will get the tangent of that angle as we know that:
$\cot \theta = $$\dfrac{{\cos \theta }}{{\sin \theta }}$

So we get the value of $\cot 60^\circ = $$\dfrac{1}{{\sqrt 3 }}$

Note:
Here in these types of problems where we are asked to find the value of the tangent or cotangent of any angle, we must know the basic values of the sine and cosine of the angles like $0^\circ ,30^\circ ,45^\circ ,60^\circ ,90^\circ $ and then we can easily calculate the same angles of the tangent, cotangent, secant, and cosecant of that same angle.