Question

Find the value of $\cos ec$${{30}^{\circ }}$ geometrically?

Answer 1

Hint: Before starting the question, it is very important to learn all the definitions of all the $6$ trigonometric ratios which are $\sin ,\cos ,\tan ,\sec ,\cos ec,\cot $. To find the value of $\cos ec$${{30}^{\circ }}$ geometrically, we need to make us of an equilateral triangle. We all know that an equilateral triangle is a type of triangle in which all sides are equal. We drop a perpendicular from one vertex to it’s opposite side. We make use of some properties of the triangle and then find the value of $\cos ec$${{30}^{\circ }}$.

Complete step by step solution:
Picture for reference :

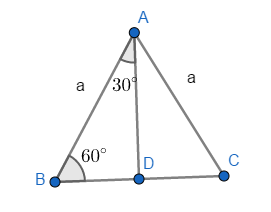
Let us take a triangle $ABC$ which is an equilateral triangle.
Let the length of the side be $a$.
Now let us drop a perpendicular named $AD$ from vertex $A$ to the opposite side $BC$.
We know that in an equilateral triangle the medians, perpendiculars and angular bisectors over-lap and are the same. So our perpendicular $AD$, bisects the side $BC$. And the mid-point is $D$. The perpendicular also bisects the apex angle which is $A$.
$\angle BAD=\angle DAC=\dfrac{{{60}^{\circ }}}{2}={{30}^{\circ }}$
$BD=DC=\dfrac{a}{2}$.
We know that the $\angle ADB={{90}^{\circ }}$.
We know that the definition of $\cos ec\theta $.
It is the following :
$\cos ec\theta =\dfrac{hypotenuse}{opposite}$.
And in this case our $\theta $ is ${{30}^{\circ }}$ .
From the $\Delta BAD$ ,
$\cos ec{{30}^{\circ }}=\dfrac{hypotenuse}{opposite}=\dfrac{AB}{BD}=\dfrac{a}{\left( \dfrac{a}{2} \right)}=2$ .
$\therefore $ Hence, the value of $\cos ec$${{30}^{\circ }}$ geometrically is $2$.

Note: We should remember all the definitions of all the $6$ trigonometric ratios so as to solve the questions quickly. If not $6$, we should be well-versed with definitions and all the values of $\sin ,\cos ,\tan $. If we inverse these $3$, we would get $co\sec ,\sec ,\cot $ respectively. We should be very careful doing calculations as it may lead to wrong results. It is very important to know all the other trigonometric identities and formulae.