Question

How do you find the value of $\cos \dfrac{\pi }{6}$?

Answer 1

Hint:
Start with assuming an equilateral triangle $\Delta MNP$ and make a perpendicular MO which divides the side NP into two equal parts NO and OP. This gives you $\angle PMO = 30^\circ $ . Now use the definition of the cosine function, find the expression for it. Now substitute the values in it and simplify it to get the required value of $\cos \dfrac{\pi }{6}$ .

Complete Step by step Solution:
Here in this question, we are given an expression in cosine function, i.e. $\cos \dfrac{\pi }{6}$ and we have to find the value for this expression.
Before starting with the solution, we must understand a few concepts about cosine functions. Cos function (or cosine function) in a triangle is the ratio of the adjacent side to that of the hypotenuse. The cosine function is one of the three main primary trigonometric functions. In a right-triangle, cos is defined as the ratio of the length of the adjacent side to that of the longest side i.e. the hypotenuse.
As we know that an angle of $\pi $ radians is equal to $180^\circ $ angle.
$ \Rightarrow \cos \dfrac{\pi }{6} = \cos \left( {\dfrac{{180^\circ }}{6}} \right) = \cos 30^\circ $
For finding this value, we first take an equilateral triangle $\Delta MNP$ with a side of length ‘m’ units. In this triangle, we have a perpendicular bisector $MO$, that divides side NP into two equal parts. We know that an equilateral has all three interior angles equal and of measure $60^\circ $ .
$ \Rightarrow NO = OP = \dfrac{{NP}}{2} = \dfrac{m}{2}$ and $\angle PMO = \dfrac{{\angle PMN}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ $
This information can be represented in a diagram as:

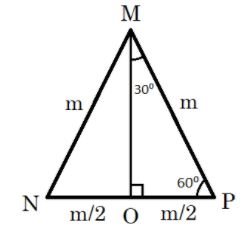
Now taking the right-angle triangle $\Delta PMO$ into consideration, we know that $PM = m{\text{ and }}OP = \dfrac{m}{2}$
We can use the Pythagoras theorem, which states that the square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides. By this theorem, in the triangle $\Delta PMO$ , we get:
$ \Rightarrow P{M^2} = M{O^2} + O{P^2}$
Now let’s substitute the known values in this equation:
$ \Rightarrow P{M^2} = M{O^2} + O{P^2} \Rightarrow {m^2} = M{O^2} + {\left( {\dfrac{m}{2}} \right)^2}$
This equation can be easily solved to find the unknown length of perpendicular MO
$ \Rightarrow {m^2} = M{O^2} + {\left( {\dfrac{m}{2}} \right)^2} \Rightarrow M{O^2} = {m^2} - \dfrac{{{m^2}}}{4} = \dfrac{{3{m^2}}}{4}$
Taking square root on both the sides, we have:
$ \Rightarrow \sqrt {M{O^2}} = \sqrt {\dfrac{{3{m^2}}}{4}} \Rightarrow MO = \dfrac{{\sqrt 3 }}{2}m$
Therefore, we get the length of the perpendicular MO as $\dfrac{{\sqrt 3 }}{2}m$
Now, according to the definition of the cosine function, we have the relation:
$ \Rightarrow \cos \theta = \dfrac{{Base}}{{Hypotenuse}}$
For the triangle $\Delta PMO$, using cosine function in angle $\angle PMO$, we can write it as:
$ \Rightarrow \cos 30^\circ = \dfrac{{Base}}{{Hypotenuse}} = \dfrac{{MO}}{{PM}} = \dfrac{{\dfrac{{\sqrt 3 }}{2}m}}{m}$
This can be simplified by dividing numerator and denominator by ‘m’
$ \Rightarrow \cos 30^\circ = \dfrac{{\dfrac{{\sqrt 3 }}{2}m}}{m} = \dfrac{{\sqrt 3 }}{2}$

Therefore, we get the required value of $\cos \dfrac{\pi }{6}$ or $\cos 30^\circ $ as $\dfrac{{\sqrt 3 }}{2}$

Note:
In this question, we used an example of an equilateral triangle that was a crucial part of the solution. Notice that the value of $\cos 30^\circ $ does not depend on the sides of the triangle. An alternative approach to this problem can be to find the value of $\sin 30^\circ $ and then use the relation ${\sin ^2}\theta + {\cos ^2}\theta = 1$ .