
Find the value of $\cos 1{}^\circ \cos 2{}^\circ \cos 3{}^\circ ..........\cos 180{}^\circ $.
Answer
614.1k+ views
Hint: We will try to trace the value of $\cos \theta $ in the first quadrant and second quadrant using its graph. And finally multiply all the values to get the result. We will also check whether any value $\theta $ of $\cos \theta $ is $0$ and if it is then it will change all the values because all the values are in multiplication with each other anything multiplied by zero is zero.
Complete step by step answer:
It is given in the question that to find the value of $\cos 1{}^\circ \cos 2{}^\circ \cos 3{}^\circ ..........\cos 180{}^\circ $. All the values of $\cos \theta $ are in multiplication with each other. Now, we will check the nature of $\cos \theta $ in the first quadrant and second quadrant.
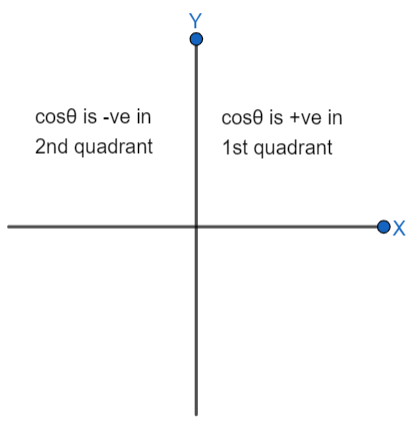
$\begin{align}
& \cos 1=+cos(179) \\
& cos2=+cos(178) \\
& cos3=+cos(177) \\
\end{align}$
And so on
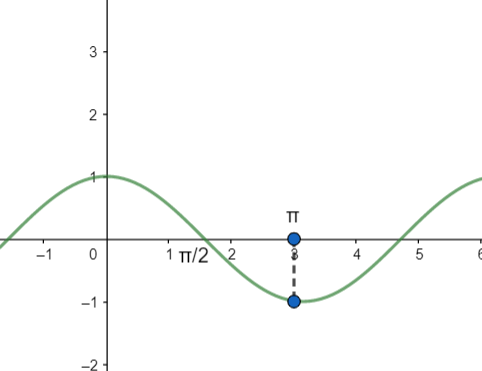
But we will look at the value of $\cos 90{}^\circ $ that is $0$. As, the value of $\cos 90{}^\circ $ is zero. When the value of $\cos 90{}^\circ $ is multiplied by any term it will become zero.
Therefore, the whole equation will be zero.
Note: Students may not solve these types of questions in example because most of them think that it is very long and time consuming but, if we understand what actually the question has demanded. Then, it can be solved even orally. The question is not lengthy but tricky. So, use your own intelligence to solve such questions.
Complete step by step answer:
It is given in the question that to find the value of $\cos 1{}^\circ \cos 2{}^\circ \cos 3{}^\circ ..........\cos 180{}^\circ $. All the values of $\cos \theta $ are in multiplication with each other. Now, we will check the nature of $\cos \theta $ in the first quadrant and second quadrant.

$\begin{align}
& \cos 1=+cos(179) \\
& cos2=+cos(178) \\
& cos3=+cos(177) \\
\end{align}$
And so on
But we will look at the value of $\cos 90{}^\circ $ that is $0$. As, the value of $\cos 90{}^\circ $ is zero. When the value of $\cos 90{}^\circ $ is multiplied by any term it will become zero.
Therefore, the whole equation will be zero.

Note: Students may not solve these types of questions in example because most of them think that it is very long and time consuming but, if we understand what actually the question has demanded. Then, it can be solved even orally. The question is not lengthy but tricky. So, use your own intelligence to solve such questions.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




