Question

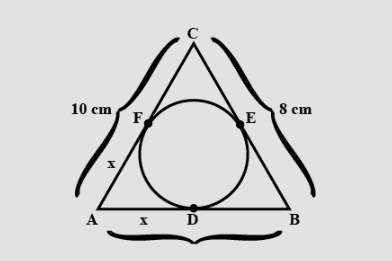
Find the value of $AD,BF$ and $CF$ in the given figure.
  

Answer 1

Hint: Use the rule of the tangents drawn from an external point to a circle subtended are equal.

Complete step-by-step answer:
We are going to use the rule that tangents drawn from an external point to a circle are equal.
Therefore,
$ \Rightarrow AD = AF,BD = BE$ and $CE = CF$
Now let us take,
$ \Rightarrow AD = AF = a$,
$ \Rightarrow BD = BE = b$ and,
$ \Rightarrow CE = CF = c$,
Add and, we get,
$AB = AD + DB = a + b = 8$ …..(1)
$BC = BE + EC = b + c = 10$ …..(2)
$AC = AF + FC = a + b = 12$ …..(3)
Add (1), (2) and (3), we get,
$2\left( {a + b + c} \right) = 30$
Taking the numbers on one side and variable on the other, we have,
$\left( {a + b + c} \right) = \frac{{30}}{2} = 15$…..(4)
Now, we are going to use (1), (2), (3) and (4), to find the value of the variables.
Subtracting (1) from (4), we get $c = 7$
Subtracting (2) from (4), we get $a = 5$
Subtracting (3) from (4), we get $b = 3$
Therefore,
$AD = a = 5cm$,
$BE = b = 3cm$
And, $CF = c = 7cm$
Note: We started by taking the rule of tangents drawn from external points to circle are equal, using this we formed equations and then solved it to get the values.