Question

Find the value of \[(A \cap B) \cap C\]

Answer 1

Hint: Associative Law states that the grouping of set operations does not change the result of next grouping of sets. It is one of the important concepts of set theory. If we have three sets A, B and C, then,
Associative Law for the Intersection of Three Sets):
If A, B, and C are sets, then \[(A \cap B) \cap C = A \cap (B \cap C).\]

Complete step-by-step answer:
Given three sets A, B and C, the intersection is the set that contains elements or objects that belong to A, to B and to C at the same time.
First Law:
First law states that the intersection of a set to the intersection of two other sets is the same.
 \[(A \cap B) \cap C = A \cap (B \cap C).\]
Proof :
In the first law \[(A \cap B) \cap C = A \cap (B \cap C).\]
Step 1:
Let us take the L.H.S, \[\left( {A{\text{ }} \cap {\text{ }}B} \right){\text{ }} \cap {\text{ }}C\]
Let\[x \in (A \cap B) \cap C\]. If \[x \in (A \cap B) \cap C\]then \[x \in \left( {A{\text{ }}and{\text{ }}B} \right)\] and \[x \in C\]
\[x \in \left( {A{\text{ }} and {\text{ }}B} \right)\] and \[x \in C\]
\[x \in \left( {A{\text{ }} and {\text{ }}B} \right)\] implies \[x \in A\] and \[x \in B\]
So, we have
\[x \in A\], \[x \in B\] and \[x \in C\]
\[x \in A\] and \[x \in \left( {B{\text{ }} and {\text{ }}C} \right)\]
\[x \in A\]\[\; \cap (B \cap C)\]
\[
  x \in (A \cap B) \cap C{\text{ }} = > {\text{ }}x \in A \cap (B \cap C) \\
  \left( {A{\text{ }} \cap {\text{ }}B} \right){\text{ }} \cap {\text{ }}C \subset A \cap (B \cap C) - - - {\text{ }}1 \\
 \]
Step 2:
Let us take the R.H.S, \[\left( {B{\text{ }} \cap {\text{ }}C} \right){\text{ }} \cap {\text{ }}A\]
\[\begin{array}{*{20}{l}}
  Let{\text{ }}x \in A \cap (B \cap C).{\text{ }} \\
  If{\text{ }}x \in A \cap (B \cap C){\text{ }}then{\text{ }}x \in A{\text{ }} and {\text{ }}x \in \left( {B{\text{ }}and{\text{ }}C} \right) \\
  {x \in A{\text{ }}and{\text{ }}x \in \left( {B{\text{ }}and{\text{ }}C} \right)} \\
  {x \in \left( {B{\text{ }}and{\text{ }}C} \right){\text{ }}implies{\text{ }}x \in B{\text{ }}and{\text{ }}x \in C}
\end{array}\]
So, we have
x ∈ A, x ∈ B and x ∈ C
x ∈ (A and B) and x ∈ C
x ∈ (A and B) and C
x ∈ (A ∩ B) ∩ C
x ∈ A ∩ (B ∩ C) => x ∈ (A ∩ B) ∩ C
A ∩ (B ∩ C) ⊂ (A ∩ B) ∩ C-- 2
From equation 1 and 2
\[\left( {A{\text{ }} \cap {\text{ }}B} \right){\text{ }} \cap {\text{ }}C{\text{ }} = {\text{ }}A{\text{ }} \cap {\text{ }}\left( {B{\text{ }} \cap {\text{ }}C} \right)\]
Hence, the associative law of sets for intersection has been proved.
We write \[(A \cap B) \cap C\]

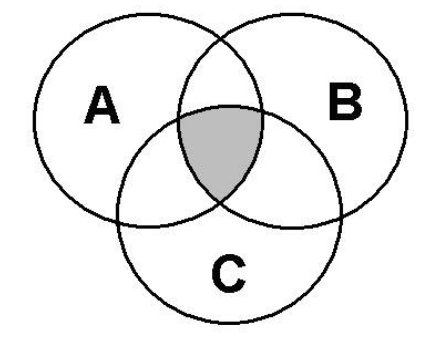
Basically, we find \[(A \cap B) \cap C\] by looking for all the elements A, B and C have in common.

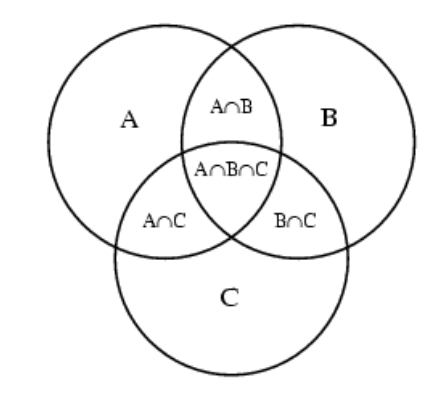
So, hence intersection of sets A, B and C has all the elements which are common to set A, Set B and Set C.

Note: To create an intersecting Venn diagram, draw three circles that overlap in the middle. You’ll be able to show which attributes are unique to each circle, which overlap between two, and which are common characteristics of all three groups.