Question

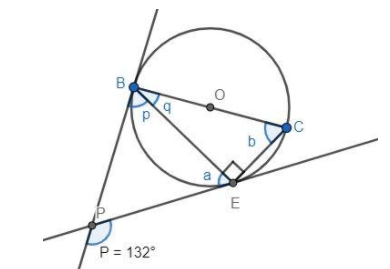
Find the value of \[a\] and \[b\].

A.\[a = 66^\circ ,b = 66^\circ \]
B.\[a = 48^\circ ,b = 66^\circ \]
C.\[a = 48^\circ ,b = 48^\circ \]
D.None of these.

Answer 1

Hint: We will use properties of tangents of a circle to prove that \[\Delta PEB\] is an isosceles triangle. We will use the exterior angle theorem to find the measure of interior angles. We will use properties of tangents of a circle to prove that \[\angle CBP\] is a right angle. We will find angle q by subtracting the measure of angle \[p\] from \[90^\circ \]. We will find the measure of angle \[b\] by using the angle sum property of a triangle.

Complete step-by-step answer:
All the tangents from an external point to a circle are equal. So, in \[\Delta PEB\], \[PE = PB\]. \[\Delta PEB\]is an isosceles triangle.
We know that the angles opposite to equal sides in an isosceles triangle are equal.
So, in \[\Delta PEB\], \[\angle p = \angle a\].
According to the exterior angle theorem, the exterior angle of a triangle is equal to the sum of 2 opposite interior angles. So, in \[\Delta PEB\]:
\[{c}132^\circ = \angle a + \angle p\\\Rightarrow 132^\circ = \angle a + \angle a\\ \Rightarrow 132^\circ = 2\angle a\\ \Rightarrow 66^\circ = \angle a\\ \Rightarrow 66^\circ = \angle p\]
We know that any tangent to a circle makes a right angle with the radius at the point where it touches the circle:
\[\angle CBP = {90^ \circ }\]
We can see from the figure that \[\angle CBP = \angle p + \angle q\]. We will compare this equation with the above equation:
\[{c}\angle p + \angle q = 90^\circ \\ \Rightarrow 66^\circ + \angle q = 90^\circ \\ \Rightarrow \angle q = 90^\circ - 66^\circ \\ \Rightarrow \angle q = 24^\circ \]
We know that the angle inscribed in a semicircle is always a right angle. So,
\[\angle CEB = 90^\circ \]
We know that according to the angle sum property of a triangle, the sum of all angles of a triangle is \[180^\circ \]. So, in \[\Delta CEB\]:
\[\angle b + \angle CEB + \angle q = 180^\circ \\ \Rightarrow \angle b + 90^\circ + 24^\circ = 180^\circ \\ \Rightarrow \angle b + 114^\circ = 180^\circ \\ \Rightarrow \angle b = 66^\circ \]
$\Rightarrow \angle a=\angle b={{66}^{\circ }}$
Option A is the correct option.

Note: We need to be aware of the properties of angles in a circle, tangent to circles and triangles to be able to solve this question. There is no definite method to solve these types of questions, we need to look at the figure and decide accordingly which property can be used to find the solution.