Question

Find the value of $1-\sin {{10}^{\circ }}\sin {{50}^{\circ }}\sin {{70}^{\circ }}$. \[\]

Answer 1

Hint: We use the reduction formula for complementary angles $\theta ,{{90}^{\circ }}-\theta $ that is $\cos \theta =\sin \left( 90-\theta \right)$ for $\theta ={{40}^{\circ }},{{20}^{\circ }}$ to convert the sines into cosines. We use the sine double angle formula $\sin 2\theta =2\sin \theta \cos \theta $ by multiplying and dividing $2\cos {{10}^{\circ }}$ with the second term and simplify until we get only term in the numerator in sine where we use $\cos \theta =\sin \left( 90-\theta \right)$ to get the answer. \[\]

Complete step by step answer:

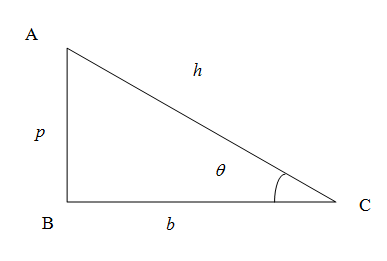
We know that in a right-angled triangle the side opposite to the right-angled triangle is called hypotenuse denoted as $h$, the vertical side is called perpendicular denoted as $p$ and the horizontal side is called the base denoted as $b$.\[\]

We know from the trigonometric ratios in a right-angled triangle the sine of any angle is given by the ratio of the side opposite to the angle to the hypotenuse. In the figure, the sine of the angle $\theta $ is given by
\[\sin \theta =\dfrac{p}{h}\]

We are asked to find the value of $1-\sin {{10}^{\circ }}\sin {{50}^{\circ }}\sin {{70}^{\circ }}$ in the question. Let use the reduction formula for complementary angles $\theta ,{{90}^{\circ }}-\theta $ that is $\cos \theta =\sin \left( 90-\theta \right)$ for $\theta ={{40}^{\circ }},{{20}^{\circ }}$ to have;
\[\begin{align}
  & \Rightarrow 1-\sin {{10}^{\circ }}\sin {{50}^{\circ }}\sin {{70}^{\circ }} \\
 & \Rightarrow 1-\sin {{10}^{\circ }}\sin \left( {{90}^{\circ }}-{{40}^{\circ }} \right)\sin \left( {{90}^{\circ }}-{{20}^{\circ }} \right) \\
 & \Rightarrow 1-\sin {{10}^{\circ }}\cos {{40}^{\circ }}\cos {{20}^{\circ }} \\
\end{align}\]
We multiply and divide $2\cos {{10}^{\circ }}$ with the second term in the above step to have;
\[\begin{align}
  & \Rightarrow 1-\dfrac{2\sin {{10}^{\circ }}\cos {{10}^{\circ }}\cos {{40}^{\circ }}\cos {{20}^{\circ }}}{2\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\left( 2\sin {{10}^{\circ }}\cos {{10}^{\circ }} \right)\cos {{20}^{\circ }}\cos {{40}^{\circ }}\cos {{20}^{\circ }}}{2\cos {{10}^{\circ }}} \\
\end{align}\]
We use the sine double angle formula $\sin 2\theta =2\sin \theta \cos \theta $ for $\theta ={{10}^{\circ }}$ in the above step to have ;
\[\begin{align}
  & \Rightarrow 1-\dfrac{\sin {{\left( 2\times 10 \right)}^{\circ }}\cos {{20}^{\circ }}\cos {{40}^{\circ }}}{2\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\sin {{20}^{\circ }}\cos {{20}^{\circ }}\cos {{40}^{\circ }}}{2\cos {{10}^{\circ }}} \\
\end{align}\]
We multiply 2 in the numerator and denominator of the second term in the above step to have;
 \[\begin{align}
  & \Rightarrow 1-\dfrac{2\sin {{20}^{\circ }}\cos {{40}^{\circ }}\cos {{20}^{\circ }}}{2\times 2\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\left( 2\sin {{20}^{\circ }}\cos {{40}^{\circ }} \right)\cos {{20}^{\circ }}}{4\cos {{10}^{\circ }}} \\
\end{align}\]
We use the sine double angle formula $\sin 2\theta =2\sin \theta \cos \theta $ for $\theta ={{20}^{\circ }}$ in the above step to have;
 \[\begin{align}
  & \Rightarrow 1-\dfrac{2\sin {{20}^{\circ }}\cos {{40}^{\circ }}\cos {{20}^{\circ }}}{2\times 2\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\sin \left( 2\times {{20}^{\circ }} \right)\cos {{40}^{\circ }}}{4\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\sin {{40}^{\circ }}\cos {{40}^{\circ }}}{4\cos {{10}^{\circ }}} \\
\end{align}\]
We multiply 2 in the numerator and denominator of the second term in the above step to have;
\[\begin{align}
  & \Rightarrow 1-\dfrac{2\sin {{40}^{\circ }}\cos {{40}^{\circ }}}{2\times 4\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{2\sin {{40}^{\circ }}\cos {{40}^{\circ }}}{8\cos {{10}^{\circ }}} \\
\end{align}\]
We use the sine double angle formula $\sin 2\theta =2\sin \theta \cos \theta $ for $\theta ={{40}^{\circ }}$ in the above step to have;
 \[\begin{align}
  & \Rightarrow 1-\dfrac{\sin {{\left( 2\times 40 \right)}^{\circ }}}{2\times 4\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\sin {{80}^{\circ }}}{8\cos {{10}^{\circ }}} \\
\end{align}\]
We use the reduction formula of complimentary angles $\cos \theta =\sin \left( 90{}^{\circ }-\theta \right)$ for $\theta ={{10}^{\circ }}$in the above step to have
\[\begin{align}
  & \Rightarrow 1-\dfrac{\sin \left( {{90}^{\circ }}-{{10}^{\circ }} \right)}{8\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{\cos {{10}^{\circ }}}{8\cos {{10}^{\circ }}} \\
 & \Rightarrow 1-\dfrac{1}{8}=\dfrac{8-1}{8}=\dfrac{7}{8} \\
\end{align}\]
So the obtained value of $1-\sin {{10}^{\circ }}\sin {{50}^{\circ }}\sin {{70}^{\circ }}$ is $\dfrac{7}{8}$. \[\]
Note:
We can alternatively solve using product of sines formula in terms cosine difference and sum of angles as $\sin A\sin B=\dfrac{1}{2}\left[ \cos \left( A-B \right)-\cos \left( A+B \right) \right]$ and then proceed to use again product of sine and cosine$\sin A\cos B=\dfrac{1}{2}\left[ \sin \left( A+B \right)-\sin \left( A-B \right) \right]$. We can also quickly find the answer if we know the formula $\sin A\sin \left( {{60}^{\circ }}-A \right)\sin \left( {{60}^{\circ }}+A \right)=\dfrac{1}{4}\sin 3A$ and use it for $A={{10}^{\circ }}$.