Question

Find the total surface area of a hollow cylinder open at both the ends, if its length is 12cm, external diameter is 8cm and the thickness is 2cm.

Answer 1

- Hint:Here, we can understand this problem by the figure of the hollow cylinder.
  

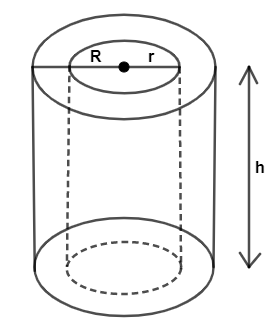
Now, height here is the length and as we can see two cylinders, radius of external cylinder is denoted by R and radius of that cylinder becomes diameter of inner cylinder which is denoted by r. We will use formula of total surface area as $2\pi h\left( R+r \right)+2\pi \left( {{R}^{2}}-{{r}^{2}} \right)$ .

Complete step-by-step solution -

In the question, it is asked to find the total surface area of a hollow cylinder, so we cannot consider one cylinder and calculate directly the surface area of the cylinder. We have to consider two cylinders one inside the other which is open at both the ends.
Here, length is given which is basically height h of cylinder. External diameter d is given 8cm which when divided by 2 becomes radius R i.e. $R=\dfrac{d}{2}=\dfrac{8}{2}=4cm$

Now, from this figure we can see that the external radius of the cylinder becomes the diameter of the inner cylinder. So, we need to find radius of inner cylinder i.e. $r=\dfrac{R}{2}=\dfrac{4}{2}=2cm$
Now, we have all the parameters with us $h=12cm,R=4cm,r=2cm$

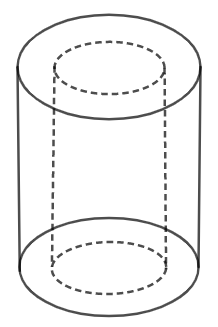
We want the total area between dotted cylinder and external cylinder. So, we will take lateral surface area of both cylinder which will be $2\pi Rh+2\pi rh$ and subtracting the base which is circle from external cylinder which will get, $2\pi {{R}^{2}}-2\pi {{r}^{2}}$
So, Total surface area of hollow cylinder $=$ Lateral surface area + area of solid bases
$=2\pi Rh+2\pi rh+2\pi {{R}^{2}}-2\pi {{r}^{2}}h$
$=2\pi h\left( R+r \right)+2\pi \left( {{R}^{2}}-{{r}^{2}} \right)$
$=2\times \dfrac{22}{7}\times 12\left( 4+2 \right)+2\times \dfrac{22}{7}\left( {{4}^{2}}-{{2}^{2}} \right)$
Taking $2\times \dfrac{22}{7}$ common, so
$=2\times \dfrac{22}{7}\times \left[ 12\left( 4+2 \right)+\left( {{4}^{2}}-{{2}^{2}} \right) \right]$
$=2\times \dfrac{22}{7}\times \left[ 72+\left( 16-4 \right) \right]$
$=2\times \dfrac{22}{7}\times \left[ 72+12 \right]$
$=2\times \dfrac{22}{7}\times 84$
$=2\times 22\times 12$
$=528c{{m}^{2}}$
Thus, the total surface area of the hollow cylinder is $528c{{m}^{2}}$ .

Note: Be careful while finding total surface area (TSA) of cylinder and hollow cylinder as it is almost similar by formula. TSA of cylinder $=2\pi rh+2\pi {{r}^{2}}$ which is lateral surface area of cylinder plus area of 2 circles. While in hollow cylinder bases are subtracted from external cylinder and are added to lateral surface area of two cylinder i.e. $=2\pi Rh+2\pi rh+2\pi {{R}^{2}}-2\pi {{r}^{2}}h$ .