Question

Find the total surface area of a cuboid whose length, breadth and height are 20 cm, 12 cm and 9 cm respectively.

Answer 1

Hint: In this question, we first need to draw the diagram with the given dimensions. Then using the formula of total surface area of a cuboid which is given by \[A=2\left( lb+bh+lh \right)\]. Now, substitute the respective values and simplify further to get the result.

Complete step-by-step answer:
Let us first assume the total surface area of the cube as A, height of the cuboid as h, length of the cuboid as l and breadth of the cuboid as b.
Now, let us draw a cuboid with the given dimensions

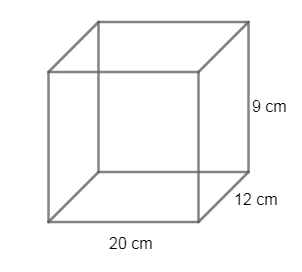
SOLID FIGURES:
The objects which occupy space that means they have three dimensions are called solids.
CUBOID:
A figure which is surrounded by six rectangular surfaces is called cuboid.
Total surface area of a cuboid is given by the formula
\[A=2\left( lb+bh+lh \right)\]
Now, from the given dimensions in the question we have
\[l=20,b=12,h=9\]
Let us now substitute these dimensions in the total surface area of cuboid formula
\[\Rightarrow A=2\left( lb+bh+lh \right)\]
Now, on substituting the respective values further we get,
\[\Rightarrow A=2\left( 20\times 12+12\times 9+9\times 20 \right)\]
Let us now multiply the corresponding terms and simplify it further
\[\Rightarrow A=2\left( 240+108+180 \right)\]
Now, on further simplifying the terms inside the bracket we get,
\[\Rightarrow A=2\times 528\]
Now, on simplifying it further we get,
\[\therefore A=1056c{{m}^{2}}\]

Note: It is important to note that we need to find the total surface area not lateral surface area. Because using the formula of the lateral surface area changes the result completely.
It is also to be noted that we should not neglect any of the terms while calculating the area. If it does it either gives only lateral surface area or another result which is incorrect.