Question

Find the total cost of leveling the shaded path of uniform width 2m, laid in the rectangular field shown below, if the rate per meter square is Rs.100.

Answer 1

Hint: A rectangle is a polygon having four sides and four vertices. All the sides are at right angles. It is also known as equiangular quadrilateral since it’s all angles are equal, and opposite sides are parallel as well. The two parallel sides of rectangles have the same dimension, which is different from the dimension of other parallel lines. The area of a rectangle is given by\[A = L \times B\]where L is the length of the rectangle and B being its breadth and \[L > B\].
In this question, if we cut the shaded paths, we get perfect rectangles. The area of each rectangle is added up which is the area of the total path hence the total cost is calculated from the given per meter square rate.

Complete step by step answer:
In the given shaded path the width is 2m.

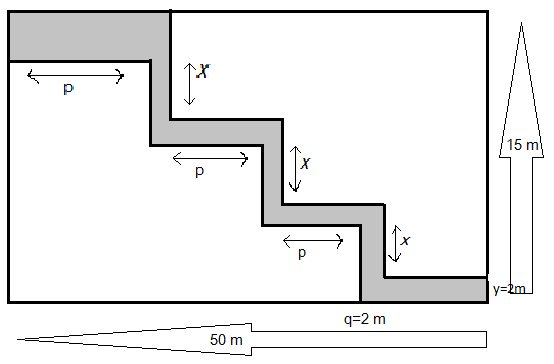
Now if we see the field vertically whose total given length is 15 meters, we can see there are four paths of 2 meters as $y$ and three unknown lengths, consider it as \[x\]; hence we can write a relation from the information as:
  \[
  15 = 3x + 4 \times y \\
  15 = 3x + 4 \times 2 \\
  15 = 3x + 8 \\
  3x = 15 - 8 \\
  x = \dfrac{7}{3} \\
 \]
Now considering the horizontal dimension which is given as 50m, here we can see three paths of 2m as \[q\] and the four unknown lengths as\[p\]hence we can equate it as
\[
  50 = 4p + 3q \\
  50 = 4p + 3 \times 2 \\
  50 = 4p + 6 \\
  4p = 50 - 6 \\
  p = \dfrac{{44}}{4} \\
   = 11 \\
 \]
Hence we calculate the total area of the shaded path by:
\[
  A = \left( {4 \times p + 3\left( {x + 4} \right)} \right) \times 2 \\
   = \left( {4 \times 11 + 3\left( {\dfrac{7}{3} + 4} \right)} \right) \times 2 \\
   = \left( {44 + 3\left( {\dfrac{{7 + 12}}{3}} \right)} \right) \times 2 \\
   = \left( {44 + 21} \right) \times 2 \\
   = 65 \times 2 \\
   = 130{m^2} \\
 \]
So total cost of leveling the 2m path will be\[ = 130 \times 100 = Rs.130000\]

Note:
 For an irregular shape whenever the area is asked first we try to break the shape into polygons and then the area of each polygon is found and then their total area is calculated.