Question

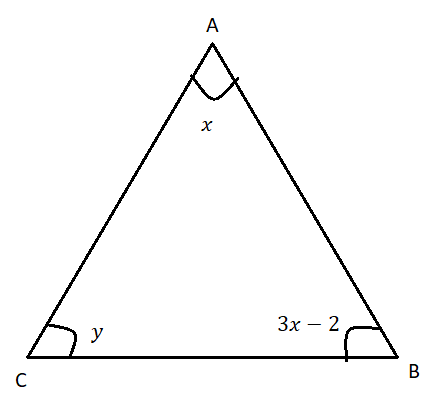
Find the three angles. If in a $\Delta ABC$,$\angle A = x,\angle B = (3x - 2),\angle C = y$. Also $\angle C - \angle B = 9$.

Answer 1

Hint:- In this question first we need to find the relation between the x and y. Then we have to use the property of the triangle which says that the sum of the interior angles of the triangle is ${180^ \circ }$. Then find the variables x and y. Finally, put values of x and y in given conditions to get the values of angles of the triangle.

Complete step-by-step answer:
We have, in $\Delta ABC$
$\angle A = x$ -- eq.1
$\angle B = (3x - 2)$ --- eq.2
$\angle C = y$ ---- eq.3
$
  \angle C - \angle B = 9 \\
   \Rightarrow y - (3x - 2) = 9 \\
   \Rightarrow y - 3x = 7{\text{ }} \\
   \Rightarrow {\text{y = 3x + 7 ---- eq}}{\text{.4}} \\
$
We know, the sum of interior angles of a triangle is ${180^ \circ }$

Using above property of triangle on $\Delta ABC$, we can write that
$ \Rightarrow \angle A + \angle B + \angle C = {180^ \circ }$
Now, put values of angles from eq. 1, eq.2, eq.3 into above equation we get
$ \Rightarrow x + (3x - 2) + y = {180^ \circ }$
Now put value of y from eq.4 into above equation we get
$
   \Rightarrow 4x - 2 + (7 + 3x) = {180^ \circ } \\
   \Rightarrow 7x = {175^ \circ } \\
   \Rightarrow x = {25^ \circ } \\
 $
Now, put value of x in eq.4 we get
$
   \Rightarrow y = 7 + 3x \\
   \Rightarrow y = {(7 + 3 \times 25)^ \circ } \\
   \Rightarrow y = {82^ \circ } \\
$
Now, put values of x, y in eq.1, eq.2, eq.3 to get values of angles
Now, to find value of angle A put value of x in eq.1, we get
$ \Rightarrow \angle A = x = {25^ \circ }$
Now, to find value of angle B put value of x in eq.2, we get
$
   \Rightarrow \angle B = 3x - 2 = 3 \times {25^ \circ } - 2 \\
   \Rightarrow \angle B = {73^ \circ } \\
$
Now, to find value of angle C put value of x in eq.3, we get
$ \Rightarrow \angle C = y = {82^ \circ }$
Hence the three angles of the triangle are ${25^ \circ },{73^ \circ },{82^ \circ }$.

Note:- Whenever you get this type of question the key concept to solve this is to learn the properties of different shapes. And remember one more thing: how to use the substitution method to find the angles of a triangle when there is a relation given between them.