Question

Find the third vertex of a $\Delta ABC$ if two of its vertices are B(-3,1) and C(0,-2) and its centroid is at the origin.

Answer 1

Hint: Start by drawing the diagram of the situation given in the figure and let the third vertex of the triangle be A(h,k). We know that the coordinate of the centroid is one third of the sum of the corresponding coordinates of the vertices of a triangle. For example: x-coordinate of centroid is equal to one third of the sum of x-coordinates of A, B and C.

Complete step-by-step answer:
Before starting the solution to the above question, let us know about the centroid of a triangle. The centroid of a triangle is defined as the meet point of the medians of the triangles drawn from the three of its vertices. The centroid of a triangle is generally denoted by G.
Now let us start the solution to the above question by drawing a diagram of the situation given in the question for better visualisation.

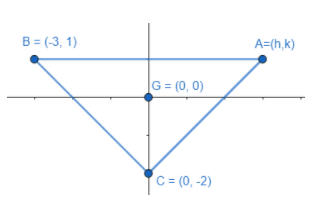
Let the third vertex of the triangle be A(h,k). We know that the coordinate of the centroid is one third of the sum of the corresponding coordinates of the vertices of a triangle.
So, we can say that the x-coordinate of centroid is equal to one third of the sum of x-coordinates of A, B and C.
$0=\dfrac{h+\left( -3 \right)+0}{3}$
$\Rightarrow h-3=0$
$\Rightarrow h=3$
Now let us move to the y-coordinate of G. We can say that the y-coordinate of centroid is equal to one third of the sum of y-coordinates of A, B and C.
$0=\dfrac{1+\left( -2 \right)+k}{3}$
$\Rightarrow k-1=0$
$\Rightarrow k=1$
Therefore, we can conclude that A=(3,1).


Note:Don’t get confused between the properties of different special points related to triangles like centroid, incentre, circumcentre etc. It is also important that you learn all the properties related to different special points as they are used very often.