Question

How do you find the third side of a right triangle if the base is x = 20m and height is y = 20m?

Answer 1

Hint: Draw a rough diagram of a right-angle triangle ABC right angled at B. Now, assume the side BC as base and AB as height of the triangle. Apply the Pythagoras theorem given as: - base\[^{2}\] + perpendicular\[^{2}\] = hypotenuse\[^{2}\] and substitute the values of base and perpendicular as 20 each and calculate the value of hypotenuse to get the answer.

Complete answer:
Here, we are provided with a right-angle triangle with the length of its base equal to 20m and length of its height equal to 20m. We have to determine the third side, that is hypotenuse of this triangle.
Now, let us draw a diagram of the given situation. So, we have,

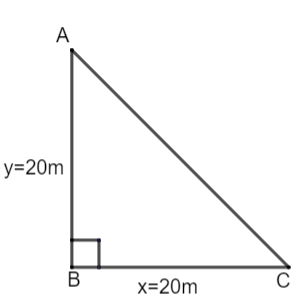
In the above figure we have assumed a right-angle triangle ABC right angled at B. We have considered BC as the base whose length is x = 20m and AB as the height or perpendicular whose length is y = 20m. AC is the hypotenuse whose length is unknown.
Now, we know that we can apply the Pythagoras theorem in a right-angle triangle to determine the unknown side if the length of the other two sides are given. So, we have,
In \[\Delta ABC\],
AB = y = 20m = perpendicular (height) = p
BC = x = 20m = base = b
Applying Pythagoras theorem given as: - \[{{p}^{2}}+{{b}^{2}}={{h}^{2}}\], we have,
\[\Rightarrow {{h}^{2}}\] = hypotenuse\[^{2}\]
\[\begin{align}
  & \Rightarrow {{h}^{2}}=A{{C}^{2}} \\
 & \Rightarrow {{p}^{2}}+{{b}^{2}}=A{{C}^{2}} \\
 & \Rightarrow A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} \\
 & \Rightarrow A{{C}^{2}}={{y}^{2}}+{{x}^{2}} \\
 & \Rightarrow A{{C}^{2}}={{\left( 20 \right)}^{2}}+{{\left( 20 \right)}^{2}} \\
\end{align}\]
\[\Rightarrow A{{C}^{2}}=2\times {{\left( 20 \right)}^{2}}\]
Taking square root both sides, we get,
\[\begin{align}
  & \Rightarrow AC=\sqrt{2\times {{\left( 20 \right)}^{2}}} \\
 & \Rightarrow AC=20\sqrt{2}m \\
\end{align}\]
Hence, the length of the third side is \[20\sqrt{2}m\].

Note: One may note that besides Pythagoras theorem we can also apply the method of trigonometry to find the length of side AC. What we can do is we will first determine the angle C by using the formula: - \[\tan C=\dfrac{y}{x}=\dfrac{20}{20}=1\]. Hence, angle C will be \[{{45}^{\circ }}\]. Now, we will use the ratio \[\sin C=\dfrac{y}{AC}\] and by substituting the known value of y = 20 and \[\sin {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}\], we will get the value of AC. You may also use \[\cos C=\dfrac{x}{AC}\] as it will not alter the answer.