Question

How do you find the terminal point $ p\left( {x,y} \right) $ on the unit circle determined by the giving value of $ t = \dfrac{{ - 3\pi }}{4} $ ?

Answer 1

Hint: In order to find the terminal point $ p\left( {x,y} \right) $ on the unit circle, start with $ \left( {1,0} \right) $ which is $ \left( {\cos {0^ \circ },\sin {0^ \circ }} \right) $ at $ {0^ \circ } $ , as we know that the general terminal point for a circle is $ p\left( {\cos x,\sin x} \right) $ . We are given with the angle of $ t = \dfrac{{ - 3\pi }}{4} $ . So just put the value of $ t $ in the place of $ x $ in $ p\left( {\cos x,\sin x} \right) $ solve and get the value in the form of $ p\left( {x,y} \right) $ , where $ p\left( {x = \cos x,y = \sin x} \right) $ .

Complete step by step solution:
We are given with the angle $ t = \dfrac{{ - 3\pi }}{4} $ .
Since, we know that the general terminal point of a unit circle is: $ p\left( {\cos x,\sin x} \right) $ .
Representing it in diagram we get:

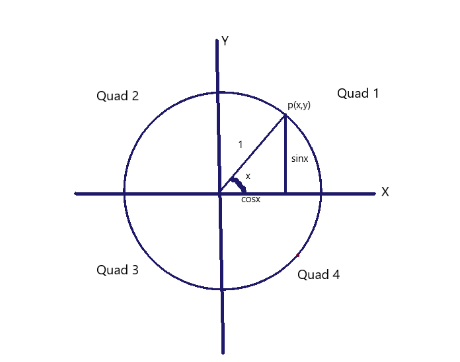
Put the value of $ t = \dfrac{{ - 3\pi }}{4} $ , in the place of $ x $ and we get:
 $ p\left( {x = \cos x,y = \sin x} \right) = p\left( {\cos \left( {\dfrac{{ - 3\pi }}{4}} \right),\sin \left( {\dfrac{{ - 3\pi }}{4}} \right)} \right) $
Solving each part of sine and cosine separately:
As we know that $ \cos \left( { - x} \right) $ is written as $ \cos x $ , with this for cosine we can write:
 $ \cos \left( {\dfrac{{ - 3\pi }}{4}} \right) = \cos \left( {\dfrac{{3\pi }}{4}} \right) $
Solving it for simplest form, to know the value we write:
\[\cos \left( {\dfrac{{3\pi }}{4}} \right) = \cos \left( {\pi - \dfrac{\pi }{4}} \right)\]
As this would give the value of cosine in 2nd Quadrant which is not the home of cosine so the value will be negative and we also know that \[\cos \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}\].Putting it in the value and we get: \[\cos \left( {\pi - \dfrac{\pi }{4}} \right) = - \cos \left( {\dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}\]
Similarly solving for sine, we get:
 $ \sin \left( {\dfrac{{ - 3\pi }}{4}} \right) = - \sin \left( {\dfrac{{3\pi }}{4}} \right) $
Solving it for simplest form, to know the value we write:
\[ - \sin \left( {\dfrac{{3\pi }}{4}} \right) = - \sin \left( {\pi - \dfrac{\pi }{4}} \right)\]
As this would give the value of sine in 2nd Quadrant which is the home of sine so the value will be positive and we also know that \[\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}\].Putting it in the value and we get: \[ - \sin \left( {\pi - \dfrac{\pi }{4}} \right) = - \sin \left( {\dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}\]
 Hence, $ p\left( {\cos x,\sin x} \right) $ becomes $ p\left( {\cos \left( {\dfrac{{ - 3\pi }}{4}} \right),\sin \left( {\dfrac{{ - 3\pi }}{4}} \right)} \right) = p\left( { - \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}} \right) $
Therefore, the terminal point $ p\left( {x,y} \right) $ on the unit circle determined by the giving value of $ t = \dfrac{{ - 3\pi }}{4} $ is: $ p\left( {\cos \left( {\dfrac{{ - 3\pi }}{4}} \right),\sin \left( {\dfrac{{ - 3\pi }}{4}} \right)} \right) = p\left( { - \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}} \right) $ where $ x = \cos \left( { - \dfrac{{3\pi }}{4}} \right) = - \dfrac{1}{{\sqrt 2 }} $ and $ y = \sin \left( { - \dfrac{{3\pi }}{4}} \right) = - \dfrac{1}{{\sqrt 2 }} $ .
So, the correct answer is “$p\left( { - \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}} \right) $ ”.

Note: Always check for the Quadrants for the sign of the values.
If the angle is positive then move counter clockwise also called anti-clockwise, and if angle is negative then move clockwise.