Question

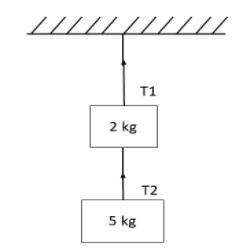
Find the tension in the string.

Answer 1

Hint: Tension is nothing but the force that acts in an axial direction. we know that the tensile force and compressive force. The tensile force means the stretching force acting on the material. The object is hung by ropes, strings, and chains, the tensile force acts in an axial direction in the ropes or strings due to the mass of the object. The tensions are to be measured here in the problem.

Formula used:
For the object, which is hung by the string and is in stationary (not moving)
The tension in the string $T = W$, $\left( {W = m \times g} \right)$
$T = m \times g$
Where T- the tension in the string
$W$- weight of the object hung by the string (N)
\[m\] - the mass of the object hung by the string
\[g\] - acceleration due to gravity $\left( {g = 9.81 \times \dfrac{m}{{{s^2}}}} \right)$


Complete answer:
We are going to find the tensions of the string $T_1,T_2$.
To find the tension $T_1$,${m_1} = 2kg$
$T_1 = {m_1} \times g$
$T_1 = 2 \times 9.81$
$T_1 = 19.62N$
The tension of the string $T_1 = 19.62N$
To find the tension $T_2,{m_2} = 5kg$
$T_2 = {m_2} \times g$
$T_2 = 5 \times 9.81$
$T_2 = 49.05N$
The tension of the string $T_2 = 49.05N$
From the above calculations, we found that the tensions of the string as a result.
$T_1 = 19.62N$,$T_2 = 49.05N$

Note: For example, if we stretch the rubber bands, it undergoes tensile force and causes tension in the rubber band. The tensile strength of the material is defined as the ability of the material by which it can sustain the maximum amount of load when being stretched. These calculations can be used in constructions and manufacturing industrial components, The tension of the string, rope, or chain during acceleration is $T = W \pm m.a$. For the object goes upward,$T = W + m.a$and for the object goes downward, $T = W - m.a$.