Question

How do you find the surface area of a rectangular prism with length $ 8cm $ , width $ 5cm $ , and height $ 4cm $ with a hold diameter $ 2cm $ drilled through it?

Answer 1

Hint: A rectangular prism consists of a three-dimensional solid shape with six rectangle-shaped faces, according to geometry. Since it has the same cross-section along its length, it is also a prism. It is, in truth, a rectangular prism.
Formulas:
Lateral Surface area of a solid rectangular prism, $ {A_l} = 2 \times \left( {bh + lh} \right) $
Base area of the prism (Top and Bottom), $ {A_{bp}} = 2lb $
Lateral Surface area of the cylinder, $ {A_c} = 2\pi rh $
Base area of the cylinder (Top and Bottom), $ {A_{bc}} = 2\pi {r^2} $

Complete step by step solution:
From the question we know that,
 $ l = 8cm $ , $ b = 5cm $ , $ h = 4cm $ and $ r = 2cm $

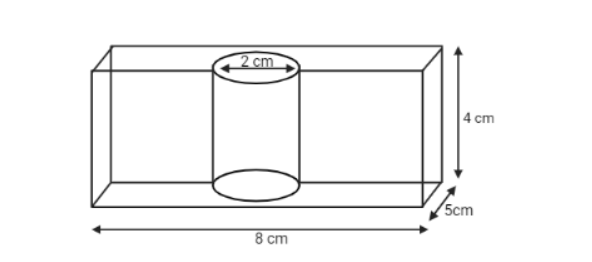
To obtain the Total surface area of the solid, we have to find the values of Lateral Surface area of a solid rectangular prism, Base area of the prism (Top and Bottom), Lateral Surface area of the cylinder, and Base area of the cylinder (Top and Bottom).
Lateral Surface area of a solid rectangular prism, $ {A_l} = 2 \times \left( {bh + lh} \right) $
 $
  {A_l} = 2 \times \left( {bh + lh} \right) \\
   = 2 \times \left( {5 \times 4 + 8 \times 4} \right) \\
   = 104c{m^2} \;
  $
Base area of the prism (Top and Bottom), $ {A_{bp}} = 2lb $
 $
  {A_{bp}} = 2lb \\
   = 2 \times 8 \times 5 \\
   = 80c{m^2} \;
  $
Lateral Surface area of the cylinder, $ {A_c} = 2\pi rh $
 $
  {A_c} = 2\pi rh \\
   = 2\pi \left( 2 \right)\left( 4 \right) \\
   = 16\pi c{m^2} \;
  $
Base area of the cylinder (Top and Bottom), $ {A_{bc}} = 2\pi {r^2} $
 $
  {A_{bc}} = 2\pi {r^2} \\
   = 2\pi \left( {2 \times 2} \right) \\
   = 8\pi c{m^2} \;
  $
Therefore, Total Surface Area of the Solid, $ TSA = {A_l} + {A_c} + {A_{bp}} - {A_{bc}} $
 $
  TSA = {A_l} + {A_c} + {A_{bp}} - {A_{bc}} \\
   = 104 + 16\pi + 80 - 8\pi \\
   = 184 - 8\pi \\
   \approx 184 - 25.132 \\
   \approx 158.868c{m^2} \;
  $
Therefore, Total Surface Area of the Solid $ = 158.868c{m^2} $
So, the correct answer is “ $ 158.868\;c{m^2} $ ”.

Note: Pyramids have triangular lateral faces, while prisms have rectangular lateral faces. Both prisms and pyramids have lateral faces that are pointed toward the base or bases in most instances. The "right prism," in which the faces are completely perpendicular to the base, is a special exception.
A right prism is a structural solid with vertical sides perpendicular to the base and a polygon as its base. The form and size of the base and top surfaces are identical.