Question

Find the surface area of a cubical box whose one side is $ 80\,cm. $

Answer 1

Hint: To find surface area of a cubical box. We first find the area of its one face, which is in square shape and then multiplying it with six to get the surface area of a given cubical box. The cubical box has six identical faces which are in a square shape of the same side as of a cube.
Surface area of a cubical box = $ 6{\left( {side} \right)^2} $

Complete step-by-step answer:
Given side of a cubical box is $ 80\,cm. $
We know that a cubical box has six faces. Which are in square shape.
Side of each square is equal to $ 80\,cm. $

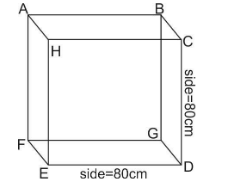
So, to find the area of a cubical box. We first find the area of its one face. Each face is in square shape.
Therefore, area of a square is given as: $ side \times side $
Substituting value of side in above. We have,
Area of one square face of a cubical box is = $ 80 \times 80 $
Area of one square face of a cubical box is = $ 6400 $
Therefore, from above we see that area of a square face of a cubical box is $ 6400\,c{m^2} $
Since, the cubical box has six identical faces.
Therefore, its surface area can be calculated by multiplying the above area of a square face by $ 6 $ .
 $ \Rightarrow area\,\,of\,\,a\,\,cubical\,\,box = 6 \times area\,\,of\,\,one\,\,face\,\,of\,\,cubical\,\,box $
 $ \Rightarrow area\,\,of\,\,a\,\,cubical\,\,box = 6 \times 6400 $
 $ \Rightarrow area\,\,of\,\,a\,\,cubical\,\,box = 38400 $ .
Hence, from above we see that area a cubical box is $ 38400\,\,c{m^2} $ .

Note: We can also find solutions to the given problem in other ways. In this we can directly use the mensuration formula of the surface area of a cube, which is $ 6{(side)^2} $ . In this formula we directly put the value of the given side of a cube to get the required surface area of a cube.