
Find the supplement of the angle ${90^ \circ }$.
Answer
581.1k+ views
Hint: If two angles are supplementary, the sum of these two angles must be equal to ${180^ \circ }$. Assume the other unknown angle to be some variable and then add it with the given angle in the question putting the resultant ${180^ \circ }$. From this equation, find the value of the unknown angle.
Complete step-by-step answer:
According to the question, the supplement of angle ${90^ \circ }$ is to be determined.
We know that the two angles are supplementary only when their sum is ${180^ \circ }$. Thus, by applying this condition and assuming the supplement of angle ${90^ \circ }$ to be a variable $x$, we’ll get:
$ \Rightarrow x + {90^ \circ } = {180^ \circ }$
Solving this equation for $x$, we’ll get:
$
\Rightarrow x = {180^ \circ } - {90^ \circ } \\
\Rightarrow x = {90^ \circ }
$
Therefore the supplement of angle ${90^ \circ }$ is also ${90^ \circ }$.
Additional information: In the above case, we have seen that the supplement angle of ${90^ \circ }$ is also ${90^ \circ }$. From this we can conclude that the line making these angles with the surface is perpendicular. This is shown in the below figure:
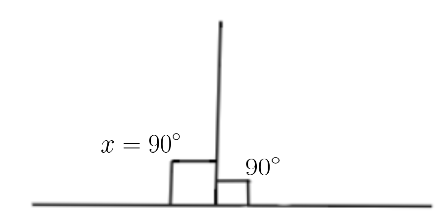
There exist another set of two angles called complementary angles. Two angles are called complementary angles when the sum of both the angles is ${90^ \circ }$. This is shown in the below figure:
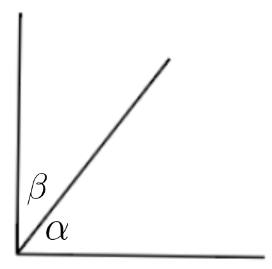
In this figure, angles $\alpha $ and $\beta $ are complementary angles. So we can conclude that:
$ \Rightarrow \alpha + \beta = {90^ \circ }$
Note: An angle is called right angle if it measures exactly ${90^ \circ }$. If an angle measures less that ${90^ \circ }$, it is called acute angle. And if an angle measures more than ${90^ \circ }$ and less than ${180^ \circ }$, it is called obtuse angle.
Complete step-by-step answer:
According to the question, the supplement of angle ${90^ \circ }$ is to be determined.
We know that the two angles are supplementary only when their sum is ${180^ \circ }$. Thus, by applying this condition and assuming the supplement of angle ${90^ \circ }$ to be a variable $x$, we’ll get:
$ \Rightarrow x + {90^ \circ } = {180^ \circ }$
Solving this equation for $x$, we’ll get:
$
\Rightarrow x = {180^ \circ } - {90^ \circ } \\
\Rightarrow x = {90^ \circ }
$
Therefore the supplement of angle ${90^ \circ }$ is also ${90^ \circ }$.
Additional information: In the above case, we have seen that the supplement angle of ${90^ \circ }$ is also ${90^ \circ }$. From this we can conclude that the line making these angles with the surface is perpendicular. This is shown in the below figure:

There exist another set of two angles called complementary angles. Two angles are called complementary angles when the sum of both the angles is ${90^ \circ }$. This is shown in the below figure:

In this figure, angles $\alpha $ and $\beta $ are complementary angles. So we can conclude that:
$ \Rightarrow \alpha + \beta = {90^ \circ }$
Note: An angle is called right angle if it measures exactly ${90^ \circ }$. If an angle measures less that ${90^ \circ }$, it is called acute angle. And if an angle measures more than ${90^ \circ }$ and less than ${180^ \circ }$, it is called obtuse angle.
Recently Updated Pages
Master Class 7 English: Engaging Questions & Answers for Success

Master Class 7 Maths: Engaging Questions & Answers for Success

Master Class 7 Science: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Trending doubts
The value of 6 more than 7 is A 1 B 1 C 13 D 13 class 7 maths CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

The plural of Chief is Chieves A True B False class 7 english CBSE

Write a letter to the editor of the national daily class 7 english CBSE





