Question

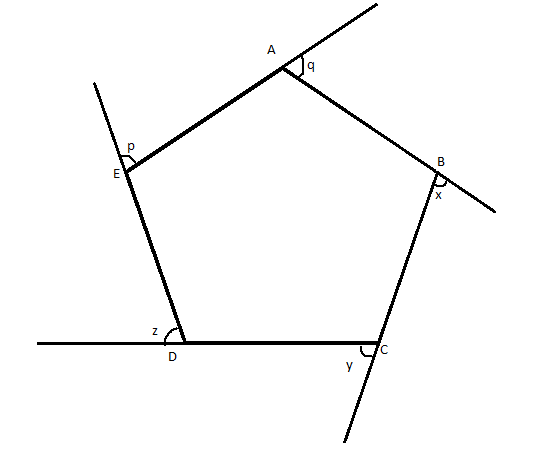
Find the sum of exterior angles \[x + y + z + p + q\]

Answer 1

Hint: Here, we have to find the sum of all exterior angles of a pentagon. We will use the properties of a pentagon and the properties of exterior angles. Since the interior and exterior angle together add up to a straight line, their values should equal 180 degrees. So, to find the measurement of an exterior angle, we will take the corresponding interior angle and subtract it from 180 degree.

Complete step-by-step answer:
We know that the exterior angle is the angle between any side of a shape, and a line extended from the next side. The sum of all exterior angles of a polygon is \[360^\circ \].
Let \[ABCDE\] be a pentagon.
Let \[x,y,z,p,q\] be the exterior angles of the sides \[BC,CD,DE,EA,AB\] of the pentagon respectively.
We know that the sum of all exterior angles of a polygon is \[360^\circ \].
\[ \Rightarrow x + y + z + p + q = 360^\circ \]
Therefore, the sum of exterior angles \[x + y + z + p + q\] is \[360^\circ \].

Note: We should know that even though the angles are not equivalent, the sum of the exterior angles of an irregular polygon also equals 360 degrees. Because irregular polygons have interior angles with different measurements, however, each exterior angle may have a different measurement as well.
If we know the value of an exterior angle of a regular polygon, we can easily find the number of sides that the polygon has as well. To do this, we would keep in mind that 360 divided by the number of sides of the polygon would result in the value of the exterior angle. Therefore, through the rule of cross multiplication, 360 divided by the value of one exterior angle would result in the number of sides of the polygon as well.