Question

Find the sum of all the exterior angles of a triangle.
(a) \[{{180}^{o}}\]
(b) \[{{270}^{o}}\]
(c) \[{{360}^{o}}\]
(d) \[{{540}^{o}}\]

Answer 1

Hint: We know that the sum of two angles on the line adds up to \[{{180}^{o}}\] . We also know that the sum of all the interior angles of the triangle is \[{{180}^{o}}\]. These two results also form the basis of another result,i.e., exterior angle measure is equal to the sum of two opposite interior angles.

Complete step by step answer:

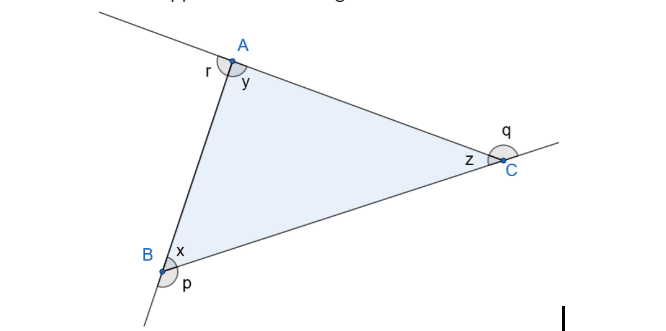
We know that the sum of two angles on a line is \[{{180}^{o}}\].
So, we can say that the following pair sums to\[{{180}^{o}}\] .
\[r+y={{180}^{o}}.............................(i)\]
\[q+z={{180}^{o}}.............................(ii)\]
\[p+x={{180}^{o}}.............................(iii)\]
We also know that the sum of all the interior angles of a triangle is \[{{180}^{o}}\].
So, we can say that sum of the angles of triangle ABC, i.e.,
\[x+y+z={{180}^{o}}.............................(iv)\]
Now, we are going to add the equations (i),(ii) and (iii). On adding these equations, we get
.\[r+y+q+z+p+x={{540}^{o}}\]
Let us now collect the interior angles x,y,z together and exterior angles p,q,r together.
 \[\Rightarrow \left( x+y+z \right)+\left( p+q+r \right)={{540}^{o}}\]
From equation (iv), we know the sum of x+y+z. Now, we will substitute the value of x+y+z. On substituting, we get the following result.
\[\Rightarrow {{180}^{o}}+\left( p+q+r \right)={{540}^{o}}\]
Now, we will subtract 180 from both sides of the above equation. We get the following result.
\[\Rightarrow \left( p+q+r \right)={{360}^{o}}\]
This is our desired result. We know that p,q, and r are exterior angles of the triangle ABC. We conclude from the above result that the sum of the exterior angles of a triangle is 360.
Hence, the (c) option is correct.

Note: We can also get to the result using an alternative way. We know that the exterior angle measure is equal to the sum of its two opposite angles. So, we get
.\[p=y+z,q=x+y,r=x+z\]
So, on adding these terms, we get the sum of exterior angles p,q,r.
p+q+r=2(x+y+z). So, this again leads to the same result. It is also worth noting that the sum of exterior angles for any polygon is 360.