Question

How do you find the standard form of the equation of the ellipse given the properties foci \[\left( {0,\, \pm 5} \right)\], vertices \[\left( {0,\, \pm 8} \right)\] ?

Answer 1

Hint: Since, the x-coordinates of both vertices and foci are given, this is an indication that these are the points of a vertical ellipse with centre at origin. We know that standard form of vertical ellipse with centre at origin is
\[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]
By using this standard equation we will get the equation of the ellipse.

Complete step-by-step solution:
The foci are on the x-axis, so the major axis is the x-axis. Thus the equation will have the form:
\[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]
The vertices are\[\left( {0,\, \pm 8} \right)\], so \[a = 8\] and \[{a^2} = 64\]
The foci are\[\left( {0,\, \pm 5} \right)\], so \[c = 5\] and\[{c^2} = 25\].
We know that the vertices and foci are related by the equation \[{c^2} = {a^2} - {b^2}\] solving for \[{b^2}\] we have
\[25 = 64 - {b^2}\]
(Substitute for \[{c^2}\] and\[{a^2}\].)
\[{b^2} = 39\]
Now we need only substitute \[{a^2} = 64\] and \[{b^2} = 39\] into the standard form of the equation. The equation of the ellipse is
\[\dfrac{{{x^2}}}{{64}} + \dfrac{{{y^2}}}{{39}} = 1\]

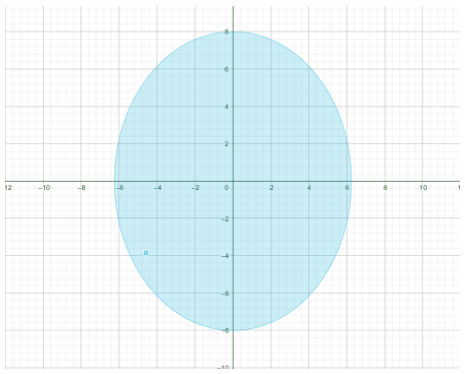
Note: Every ellipse has two axes of symmetry. The longer axis is called the major axis, and the shorter axis is called the minor axis.
Each endpoint of the major axis is the vertex of the ellipse (plural: vertices), and each endpoint of the minor axis is a co-vertex of the ellipse.
The center of an ellipse is the midpoint of both the major and minor axes. The axes are perpendicular at the center.
The foci always lie on the major axis, and the sum of the distances from the foci to any point on the ellipse (the constant sum) is greater than the distance between the foci.
STANDARD FORMS OF THE EQUATION OF AN ELLIPSE WITH CENTER \[(0,0)(0,0)\]
The standard form of the equation of an ellipse with center \[(0,0)(0,0)\] and major axis parallel to the x-axis is