Question

Find the square root of the following number by the prime factorisation method.
$5929$

Answer 1

Hint: To find the square root of the given number $5929$ by the prime factorisation method, we will write that number as the multiple of the primes. After that it will be written in the form of a group of two. Then, we will select one prime number from each group and multiply all such prime numbers. The square root of $5929$ will be the product of selected prime numbers.

Complete step-by-step answer:
To solve the given question, we must know the prime factorisation method. By using the method of prime factorisation, we can express the given number as a product of prime numbers. Therefore, we will write the given number $5929$ as the product of primes. Let us do prime factorisation of $5929$.

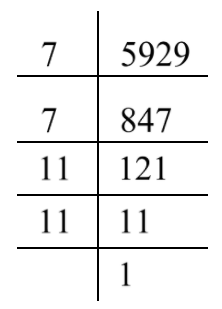
Therefore, we can write $5929 = 7 \times 7 \times 11 \times 11$.
Now we will take the same prime numbers together and write them in groups of two as shown below.
$5929 = \left( {7 \times 7} \right) \times \left( {11 \times 11} \right)$
Now we will take one number from each group. Therefore, we will get $7$ and $11$ from first group and second group respectively. Hence, the square root of $5929$ will be the product of $7$ and $11$.
Therefore, $\sqrt {5929} = \sqrt {{7^2} \times {{11}^2}} $
$ \Rightarrow \sqrt {5929} = 7 \times 11$
$ \Rightarrow \sqrt {5929} = 77$

Note: $5929$ is not an even number. So, it is not divisible by $2$. Sum of all digits of the number $5929$ is $25$ and $25$ is not divisible by $3$. So, the given number $5929$ is not divisible by $3$. The unit digit of the given number is not $0$ or $5$. So, it is not divisible by $5$. Hence, we cannot start prime factorisation by $2,3$ and $5$.