
Find the square root of the following decimal numbers:
Find the square root of the following decimal numbers:
A.2.56
B.7.29
C.51.84
D.42.25
E.31.36
Answer
615.9k+ views
Hint: Mark the period in both integral and decimal parts in a pair. After that find the square root by long division method and put the decimal point on the square root.
Complete step-by-step answer:
Let us take the first decimal number 2.56. Let us divide it with 1.
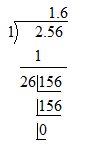
We know, \[24\times 4=96\]
\[\begin{align}
& 25\times 5=125 \\
& 26\times 6=156 \\
\end{align}\]
The square root of 2.56 = 1.6
So step 1 is to make the number of decimal places even by affixing a zero on the extreme right of the decimal part if it’s not even. As step 2, in the integral part, mark the period, \[\left( 2.\overline{56} \right)\]. In the decimal part, mark the periods on every pair of digits beginning with \[{{1}^{st}}\] decimal place. Now find the square root by long division method and put the decimal point in the square root.
Now let us find the square root of 7.29
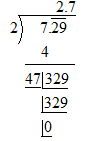
We know, \[45\times 5=225\]
\[\begin{align}
& 46\times 6=276 \\
& 47\times 7=329 \\
\end{align}\]
Square root of 51.84
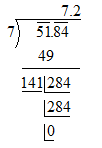
\[\left\{ \begin{align}
& 141\times 1=141 \\
& 142\times 2=284 \\
\end{align} \right.\]
\[\therefore \] We got square root of 51.84 = 7.2
Now let’s get the square root of 42.25
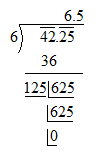
\[\left\{ \begin{align}
& 123\times 3=369 \\
& 124\times 4=496 \\
& 125\times 5=625 \\
\end{align} \right.\]
Thus square root of 42.25 = 6.5
Square root of 31.36
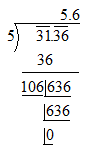
\[\left\{ \begin{align}
& 104\times 4=416 \\
& 105\times 5=525 \\
& 106\times 6=636 \\
\end{align} \right.\]
Thus we got the square root of the following decimal numbers as,
2.56 = 1.6
7.29 = 2.7
51.84 = 7.2
42.25 = 6.5
31.36 = 5.6
Note: Remember that the division of the integral part must be by a perfect square i.e. (2 \[\times \] 2), (3 \[\times \] 3), (4 \[\times \]4), (5 \[\times \] 5) etc which we have used here. Also mark the periods in both integral and decimal parts on every pair of digits.
Complete step-by-step answer:
Let us take the first decimal number 2.56. Let us divide it with 1.
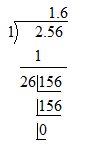
We know, \[24\times 4=96\]
\[\begin{align}
& 25\times 5=125 \\
& 26\times 6=156 \\
\end{align}\]
The square root of 2.56 = 1.6
So step 1 is to make the number of decimal places even by affixing a zero on the extreme right of the decimal part if it’s not even. As step 2, in the integral part, mark the period, \[\left( 2.\overline{56} \right)\]. In the decimal part, mark the periods on every pair of digits beginning with \[{{1}^{st}}\] decimal place. Now find the square root by long division method and put the decimal point in the square root.
Now let us find the square root of 7.29
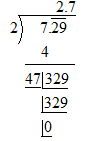
We know, \[45\times 5=225\]
\[\begin{align}
& 46\times 6=276 \\
& 47\times 7=329 \\
\end{align}\]
Square root of 51.84
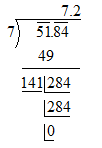
\[\left\{ \begin{align}
& 141\times 1=141 \\
& 142\times 2=284 \\
\end{align} \right.\]
\[\therefore \] We got square root of 51.84 = 7.2
Now let’s get the square root of 42.25
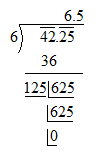
\[\left\{ \begin{align}
& 123\times 3=369 \\
& 124\times 4=496 \\
& 125\times 5=625 \\
\end{align} \right.\]
Thus square root of 42.25 = 6.5
Square root of 31.36
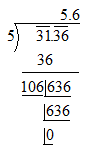
\[\left\{ \begin{align}
& 104\times 4=416 \\
& 105\times 5=525 \\
& 106\times 6=636 \\
\end{align} \right.\]
Thus we got the square root of the following decimal numbers as,
2.56 = 1.6
7.29 = 2.7
51.84 = 7.2
42.25 = 6.5
31.36 = 5.6
Note: Remember that the division of the integral part must be by a perfect square i.e. (2 \[\times \] 2), (3 \[\times \] 3), (4 \[\times \]4), (5 \[\times \] 5) etc which we have used here. Also mark the periods in both integral and decimal parts on every pair of digits.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Find the sum of series 1 + 2 + 3 + 4 + 5 + + 100 class 9 maths CBSE

Distinguish between Conventional and nonconventional class 9 social science CBSE

Find the greatest fivedigit number which is a perfect class 9 maths CBSE

Find the mode and median of the data 13 16 12 14 1-class-9-maths-CBSE




