Question

Find the square root of the following decimal number
$\left( i \right)2.56$
$\left( ii \right)7.29$
$\left( iii \right)51.84$
$\left( iv \right)42.25$
$\left( v \right)31.36$

Answer 1

Hint: To find the square root of any number, we can use a long division method. This long division method can be also used to find the square root of a decimal number. Using this method, we can solve this question.

Complete step by step answer:
To solve this question, we can use a long division method which can be used to find the square root of any real number whether it is decimal or integer.
(i) 2.56

Hence, the square root of 2.56 is 1.6.

(ii) 7.29

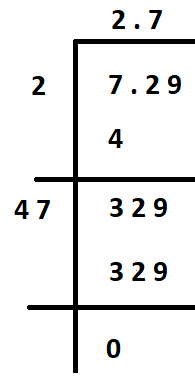
Hence, the square root of 7.29 is 2.7

(iii) 51.84

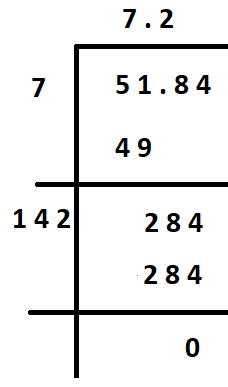
Hence, the square root of 51.84 is 7.2

(iv) 42.25

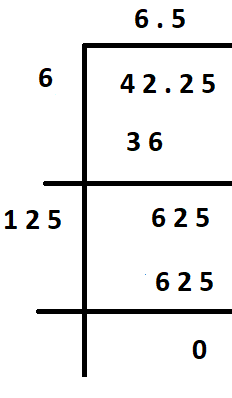
Hence, the square root of 42.25 is 6.5

(v) 31.36

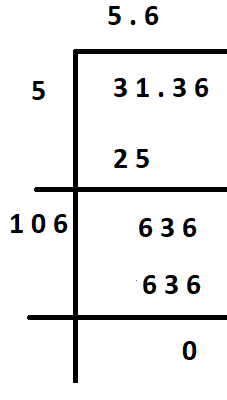
Hence, the square root of 31.36 is 5.6

Note: There is an alternate method using which, we can find the square root of a decimal number. In this method, we first convert a decimal number to the scientific form i.e. we write the decimal numbers in the form of power of 10. Now, we take the square root of this scientific form of number. We individually find the square root of the integer and the term ${{10}^{n}}$ where n is an integer. For example, if we have to find the square root of 2.56, we will first write it as $256\times {{10}^{-2}}$. Now, we will find the square root of this form which is equal to $\sqrt{256\times {{10}^{-2}}}$. This can be also written as $\sqrt{256}\times \sqrt{{{10}^{-2}}}$. We know that \[\sqrt{256}=16\] and \[\sqrt{{{10}^{-2}}}={{10}^{-1}}\]. Hence, we can write the square root of 2.56 as $16\times {{10}^{-1}}=1.6$.