Question

Find the square root of 225 by division method.
$
  {\text{A}}{\text{. 5}} \\
  {\text{B}}{\text{. 15}} \\
  {\text{C}}{\text{. 25}} \\
  {\text{D}}{\text{. 35}} \\
$

Answer 1

Hint: In order to find the square root we apply the division method, i.e. we take the largest number as the divisor whose square is less than or equal to the number on the extreme left. The number on the extreme left is the dividend. Then we divide and write the quotient and so on.

Complete step-by-step answer:
Given Data, the number is 225.
We perform division method in steps,
Step – 1:
Make a pair of digits of a given number starting with the digit at one's place. For ease of calculation; put a bar on each pair. If the number of digits of the given number is odd, then place the bar on this remaining digit also. Make pair of 25 (under bar red) and as we are left with only single digit i.e. 2, so put it under green bar (as shown below)

Step – 2:
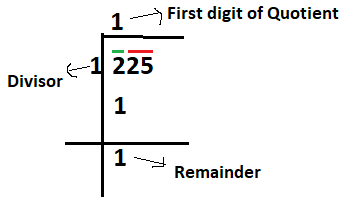
Find the divisor, such that its square is either equal or less than the number under the first bar from the left. Here the divisor and first digit of quotient will be the same. Now do the division and get the remainder. Number under the green bar i.e. 2 is the dividend. Calculated divisor is 1 and the first digit of quotient is also 1. After division we get 1 as remainder. (As shown below.)

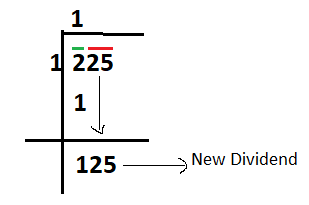
Step – 3:  Now bring down the next digits, under the second bar and place them to the right of remainder. This will become a new dividend. Bring 25 down (under red bar), place it to the right of remainder 1 (calculate in step 2) and new dividend is 125 (as shown below)

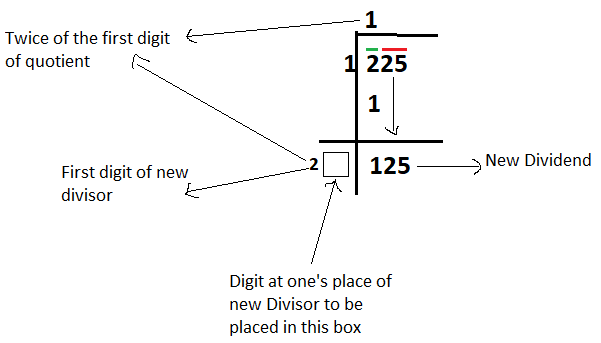
Step – 4: Starting digit(s) of new divisor is equal to twice of first digit of quotient (as in step 2) First digit of the quotient calculated in step2 is 1 and twice of 1 is 2, so 2 is the starting digit of the new divisor. (as shown below)

Step – 5:  Now the digit at one's place of new divisor is equal to the next digit of the quotient. And it is to be selected in such a way that, when new divisor is multiplied by this next digit of quotient, the product will be equal or less than the new dividend (as calculated in step 3) 5 should be the digit at one's place of new divisor because when 25 is multiplied by 5 we get 125, which is equal to our new dividend. The new divisor is 25 and the next digit of quotient is 5. (as shown below):

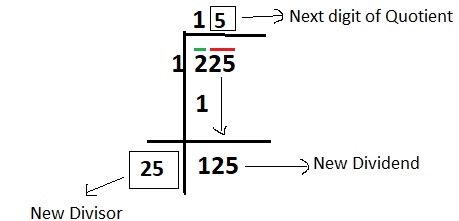
Step – 6:  Divide and get the new remainder. After division we get remainder Zero (as shown below)

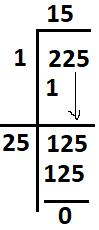
Step – 7: Since all the numbers under the bars are used, so this puts end of this method and we get 15 is the square root of 225 Or we can write it as
$\sqrt {225} = 15$
Hence, Option B is the right answer.

Note: In order to solve questions of this type the key is to apply the division method step by step in order to determine the square root. A clear understanding of the procedure of division method is required.