Question

Find the square root of 15129 by the Division Method.
(a) 117
(b) 107
(c) 123
(d) 127

Answer 1

- Hint: First of all, divide the digits into pairs of two starting from the rightmost digit. Then select the largest number as the divisor whose square is less than or equal to the pair on the extreme left. Repeat these steps after doubling the divisor each time to get the desired result.

Complete step-by-step solution -
Here, we have to find the square root of 15129
1. First of all, we have to group the digits of numbers in pairs, starting with the digits in units. For this, we will place a bar over the pair of digits starting from the unit’s digit. In the case of an odd number of digits, the leftmost digit will also have a bar.
\[\overline{1}\text{ }\overline{51}\text{ }\overline{29}\]
2. Now, we will take the largest number as the divisor whose square is less than or equal to the number on the extreme left that is 1. So, 1 is our dividend. Divide and write the quotient. Here, we will get the quotient 1 and the remainder as 0. We will do it as follows.

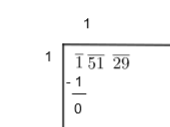
3. We then bring down the digits which are under the next bar to the right side of the remainder as follows:

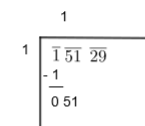
4. Now, double the value of the divisor and write it with a blank on the right side. We will do it as follows:

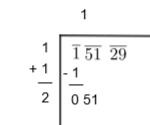
5. Now, we have to select the largest digit for the unit’s place of the divisor (2) such that the new number when multiplied by the new unit’s digit, is equal to or less than 51.
In this case, \[22\times 2=44\]. So, our digit is 2. We will do it as follows:

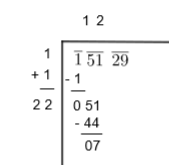
6. Now, again we will add the unit’s digit of the divisor to the value of the divisor and bring down the digits which are under the next bar to the right of the remainder as follows:

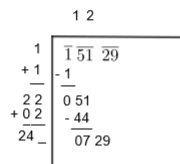
Now, we have to select the largest digit for the unit's place of the divisor (24_) such that the new number when multiplied by the new units digit, is equal to or less than 729.
7. In this case, \[243\times 3=729\]. So, our digit is 3. We will do it as follows:

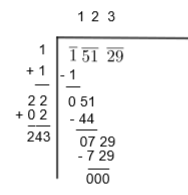
8. Now our remainder is 0 and we have no number left for multiplication.
Therefore we get \[\sqrt{15129}=123\].
Hence, the option (c) is the right answer.

Note: Students can cross-check their answer by multiplying 123 two times or squaring 123 and check if it is equal to 15129 or not, because we know that if \[a=\sqrt{15129}=123\], then \[{{a}^{2}}=15129={{\left( 123 \right)}^{2}}\]. Also, if nothing is given, students can find the square root by prime factorization of 15129. Students must note that while solving the question, we have to add units digit of the divisor to it and not double it. So, this must be taken care of.