
Find the square root of 10, correct to four places of decimal
A) \[3.4623\]
B) \[3.1023\]
C) \[3.1693\]
D) \[3.1623\]
Answer
566.7k+ views
Hint:
Here, we will solve this question by using a long division method to find the square root. Also, as we need to find it correct to four decimal places, so we will find it up to 5 decimal places and then we will round it to four decimal places.
Complete step by step solution:
As we need to find the square root correct up to 4 decimal places, we will write 10 as 10.000000000, as we take pairs of digits while calculating the square root.
In the long division method of finding the square root, we have to first find the square of a number which is closest to 10.
We know that \[{3^2} = 9 < 10\], therefore, we will divide 10 by 3 to obtain
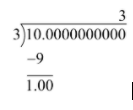
Thus, the digit before the decimal point in \[\sqrt {10} \] should be 3.
We have got the remainder as 1 and we will take down the next two digits after the decimal place.
Now, we will double the divisor in the first step that is take the divisor as 6 and we will try to find out a number of the form \[6x \times x\] is lower than but closest to 100
As \[61 \times 1 = 61 < 100\] therefore, we will divide 200 by 61 to obtain
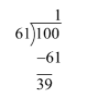
Thus, the first digit after the decimal point in \[\sqrt {10} \] should be 1.
We have got the remainder as 39 and we will take down the next two digits after the decimal place. Now, the tens place of the divisor is of the form \[60 + 1 \times 2 = 62\] as and we will try to find out a number of the form \[62x \times x\] is lower than but closest to 3900
As \[626 \times 6 = 3756 < 3900\] therefore, we will divide 3900 by 626 to obtain
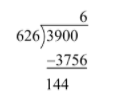
Thus, the second digit after the decimal point in \[\sqrt {10} \] should be 6.
We have got the remainder as 144 and we will take down the next two digits after the decimal place. Now, the hundreds place of the divisor is of the form \[620 + 6 \times 2 = 632\] and we will try to find out a number of the form \[632x \times x\] is lower than but closest to 14400
As \[6322 \times 2 = 12644 < 14400\] therefore, we will divide 3900 by 626 to obtain
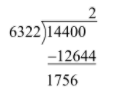
Thus, the third digit after the decimal point in \[\sqrt {10} \] should be 2.
We have got the remainder as 1756 and we will take down the next two digits after the decimal place. Now, the tens place of the divisor is of the form \[6320 + 2 \times 2 = 6324\] and we will try to find out a number of the form \[6324x \times x\] is lower than but closest to 175600
As \[63242 \times 2 = 126484 < 175600\] therefore, we will divide 175600 by 63242 to obtain
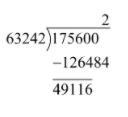
Thus, the fourth digit after the decimal point in \[\sqrt {10} \] should be 2.
We have got the remainder as 49116 and we will take down the next two digits after the decimal place. Now, the tens place of the divisor is of the form \[63240 + 2 \times 2 = 63244\] and we will try to find out a number of the form \[63244x \times x\] is lower than but closest to 4911600
As \[632447 \times 7 = 4427129 < 4911600\] therefore, we will divide 4911600 by 632447 to obtain

Thus, the fifth digit after the decimal point in \[\sqrt {10} \] should be 7.
Therefore, we have the square root of 10 as
\[\sqrt {10} = 3.16227 \approx 3.1623\]
Hence, the correct option is option D.
Note:
In this question, even though we are asked to find \[\sqrt {10} \] up to 4 decimal places, we need to find out the value of the fifth decimal place and then round it off. Because if the fifth decimal place is greater than 5, the digit obtained in the fourth place should be changed. Thus only finding the value up to four decimal places will not give us the correct answer.
Here, we will solve this question by using a long division method to find the square root. Also, as we need to find it correct to four decimal places, so we will find it up to 5 decimal places and then we will round it to four decimal places.
Complete step by step solution:
As we need to find the square root correct up to 4 decimal places, we will write 10 as 10.000000000, as we take pairs of digits while calculating the square root.
In the long division method of finding the square root, we have to first find the square of a number which is closest to 10.
We know that \[{3^2} = 9 < 10\], therefore, we will divide 10 by 3 to obtain
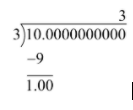
Thus, the digit before the decimal point in \[\sqrt {10} \] should be 3.
We have got the remainder as 1 and we will take down the next two digits after the decimal place.
Now, we will double the divisor in the first step that is take the divisor as 6 and we will try to find out a number of the form \[6x \times x\] is lower than but closest to 100
As \[61 \times 1 = 61 < 100\] therefore, we will divide 200 by 61 to obtain
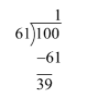
Thus, the first digit after the decimal point in \[\sqrt {10} \] should be 1.
We have got the remainder as 39 and we will take down the next two digits after the decimal place. Now, the tens place of the divisor is of the form \[60 + 1 \times 2 = 62\] as and we will try to find out a number of the form \[62x \times x\] is lower than but closest to 3900
As \[626 \times 6 = 3756 < 3900\] therefore, we will divide 3900 by 626 to obtain
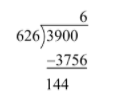
Thus, the second digit after the decimal point in \[\sqrt {10} \] should be 6.
We have got the remainder as 144 and we will take down the next two digits after the decimal place. Now, the hundreds place of the divisor is of the form \[620 + 6 \times 2 = 632\] and we will try to find out a number of the form \[632x \times x\] is lower than but closest to 14400
As \[6322 \times 2 = 12644 < 14400\] therefore, we will divide 3900 by 626 to obtain
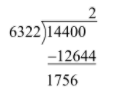
Thus, the third digit after the decimal point in \[\sqrt {10} \] should be 2.
We have got the remainder as 1756 and we will take down the next two digits after the decimal place. Now, the tens place of the divisor is of the form \[6320 + 2 \times 2 = 6324\] and we will try to find out a number of the form \[6324x \times x\] is lower than but closest to 175600
As \[63242 \times 2 = 126484 < 175600\] therefore, we will divide 175600 by 63242 to obtain
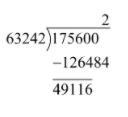
Thus, the fourth digit after the decimal point in \[\sqrt {10} \] should be 2.
We have got the remainder as 49116 and we will take down the next two digits after the decimal place. Now, the tens place of the divisor is of the form \[63240 + 2 \times 2 = 63244\] and we will try to find out a number of the form \[63244x \times x\] is lower than but closest to 4911600
As \[632447 \times 7 = 4427129 < 4911600\] therefore, we will divide 4911600 by 632447 to obtain

Thus, the fifth digit after the decimal point in \[\sqrt {10} \] should be 7.
Therefore, we have the square root of 10 as
\[\sqrt {10} = 3.16227 \approx 3.1623\]
Hence, the correct option is option D.
Note:
In this question, even though we are asked to find \[\sqrt {10} \] up to 4 decimal places, we need to find out the value of the fifth decimal place and then round it off. Because if the fifth decimal place is greater than 5, the digit obtained in the fourth place should be changed. Thus only finding the value up to four decimal places will not give us the correct answer.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




