Question

Find the square root (i) $625$ (ii) $1225$.

Answer 1

Hint: First of all, we will factorize the number with suitable numbers such as, 2, 5, 7, 11 etcetera until the remainder comes 1, and then we will represent it in tabular form. Then we will write it in general form and then the numbers which are similar we will group them as, $a\times a=\overline{a}$ and then we will multiply the grouped terms, in this way we will find the final answer.

Complete step-by-step solution -
First of all, we will write the number in tabular form and then start its factorization until the remainder is 1, which can be given as,
For 625,

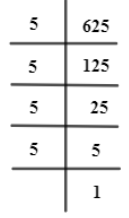
Now, this can be written in general form as,
$625=5\times 5\times 5\times 5$
Now, we will group two similar terms under one group, which can be seen as,
$625=\overline{5\times 5}\times \overline{5\times 5}$
Now, we will consider the grouped numbers as single number and on multiplying them we will get,
$625=5\times 5=25$
Hence, the square root of 625 is 25.
Now, for 1225,

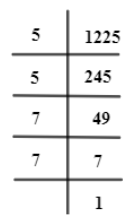
Similar, to 625, 1225 can also be written in general form as,
$1225=5\times 5\times 7\times 7$
Now, we will group two similar terms under one group, which can be seen as,
$1225=\overline{5\times 5}\times \overline{7\times 7}$
Now, we will consider the grouped numbers as single number and on multiplying them we will get,
$1225=5\times 7=35$
Hence, the square root of 1225 is 35.

Note: After converting the tabular general form, instead of grouping the similar terms, such as $625=\overline{5\times 5}\times \overline{5\times 5}$, we can also convert the similar terms in exponential form, which can be given as, $625={{5}^{4}}$ and then taking the square root of that we will get, \[625=\sqrt{{{5}^{4}}}={{5}^{2}}=25\]. Thus, this method can be considered as an alternative method.