Question

Find the square of the following numbers using diagonal method:
273.

Answer 1

Hint: Here we will use the diagonal method to calculate the square of the number. The given number has three digits. We will draw one square and will divide the square into ${{3}^{2}}$ sub squares. We will write the digits of the number on the top horizontal side of the square and left vertical side of the square. We will draw the diagonal of each square and we will multiply each digit on the left of the square with each digit on the top of column one by one. We will write the units digit of the product below the diagonal and tens digit on the top of the diagonal of the corresponding sub-squares. We will start adding the digits from bottom along the diagonals and we will write the units digit of the sum and take carry, the tens digit to the diagonal above. We will obtain the required square by writing the digits from the left most side.

Complete step-by-step answer:
The given number is 273 and it has three digits. We will draw one square and will divide the square into ${{3}^{2}}$ sub squares and we will draw the diagonal of each sub square. We will write the digits of the number on the top horizontal side of the square and left vertical side of the square.

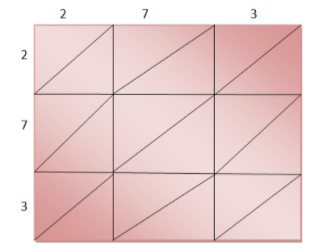
Now, we will multiply each digit on the left of the square with each digit on the top of column one by one and we will write the units digit of the product below the diagonal and tens digit on the top of the diagonal of the corresponding sub-squares.

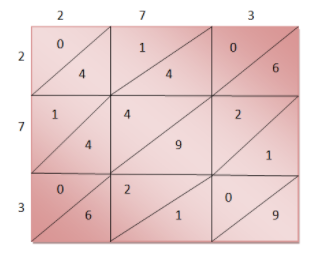
Now, we will start adding the digits from bottom along the diagonals and we will write the units digit of the sum and take carry, the tens digit to the diagonal above.

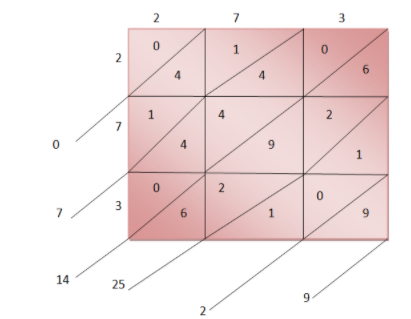
Now, we will write the digits from the left most side and this will give us the square of 273.
Therefore,
$\Rightarrow {{273}^{2}}=74529$
Hence, the square of 273 using the diagonal method is 74529.

Note: We have to be careful while adding the terms of the diagonal, we have to take carry if there is any tens digit in the sum of the digits along the diagonal. We will always take the units digit of the sum in consideration while writing the squares of the number.