Question

How do you find the smallest angle in a right-angled triangle whose side lengths are $6$ cm, $13$ cm and $14$ cm?

Answer 1

Hint: In the given question, we have been asked to find the smallest angle in a right-angled triangle whose side lengths are $6$ cm, $13$ cm and $14$ cm , we just have to use the cosine formula that is ${a^2} = {b^2} + {c^2} - bc\cos A$ here we have to find the value of ‘A’ and it is given that $a = 6,b = 13,c = 14$ . To solve this question, we need to get ‘A’ on one side of the “equals” sign, and all the other numbers on the other side. To solve this equation for a given variable ‘A’, we have to undo the mathematical operations such as addition, subtraction, multiplication, and division that has been done to the variables.

Complete step by step solution:
Since we already know that the smallest angle is always present opposite the shortest side that is $6$cm , we have to solve for the value of angle A using the Law of Cosine,

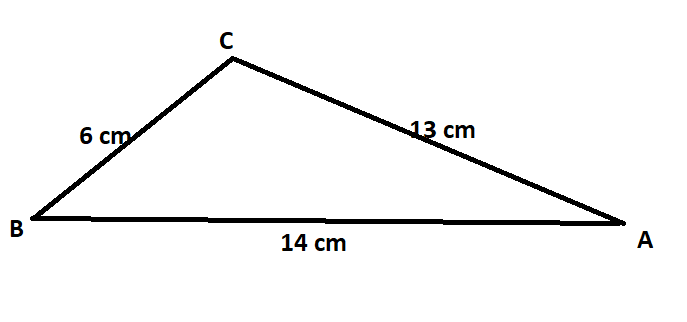
${a^2} = {b^2} + {c^2} - bc\cos A$
Where ,
$
  a = 6 \\
  b = 13 \\
  c = 14 \\
 $
Substitutes these values into the cosine formula , we will get ,
${6^2} = {13^2} + {14^2} - 2(13)(14)\cos A$
Simplify the above equation ,
$36 = 169 + 196 - 2(13)(14)\cos A$
Adding like terms , we will get ,
$36 = 365 - 364\cos A$
0r
$365 - 364\cos A = 36$
Subtract by $365$ to both the side of the equation , we will get ,
$ - 364\cos A = 36 - 365$
$ - 364\cos A = - 329$
Simplifying ,
$\cos A = \dfrac{{ - 329}}{{ - 364}}$
$\cos A = 0.9038$
$A = {\cos ^{ - 1}}(0.9038)$
$A = {25.34^ \circ }$
And hence, we get the required result.

Note: The important thing to recollect about any equation is that the ‘equals’ sign represents a balance. What the sign says is that what’s on the left-hand side is strictly an equal to what’s on the right-hand side. It is the type of question mathematical operations such as addition, subtraction, multiplication and division are used.