
how do you find the slope of the secant lines of \[f(x) = 6x - 1{x^2}\] through the points \[(2,f(2))\] and \[(2 + h,f(2 + h))\]?
Answer
526.2k+ views
Hint: First, we will use the formula of the gradient to find slope. We will put the points in the formula and try to simplify it. After that we will put the value of f(x) in that solving part and try to solve them, this will give us our answer.
Formula used: \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
Complete step by step answer:
Slope also means gradient here.
According to this question, we have to find the slope by using the two points. Here, we will use the gradient formula to find the slope or gradient. The formula is:
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
In this formula, \[({x_1},{y_1})\,\,and\,\,({x_2},{y_2})\] are the points. So, according to the question, we get:
\[({x_1},{y_1}) = (2,f(2))\] and \[({x_2},{y_2}) = (2 + h,f(2 + h))\]
Now, we will put the values or points in the formula, and we get:
\[ \Rightarrow m(h) = \dfrac{{f(2 + h) - f(2)}}{{2 + h - 2}}\]
Now, we will substitute the values \[6x - {x^2}\] in the solving part, and we get:
\[ \Rightarrow m(h) = \dfrac{{(6 - (2 + h))(2 + h) - (6 \times 2 - {2^2})}}{{2 + h - 2}}\]
Now, we will simplify the denominator, and we get:
\[ \Rightarrow m(h) = \dfrac{{(6 - (2 + h))(2 + h) - (6 \times 2 - {2^2})}}{h}\]
Now, we will simplify the numerator, and we get:
\[ \Rightarrow m(h) = \dfrac{{(4 - h)(2 + h) - (12 - 4)}}{h}\]
\[ \Rightarrow m(h) = \dfrac{{4(2 + h) - h(2 + h) - 8}}{h}\]
\[ \Rightarrow m(h) = \dfrac{{8 + 4h - 2h - {h^2} - 8}}{h}\]
\[ \Rightarrow m(h) = \dfrac{{2h - {h^2}}}{h}\]
Now, we will take \[h\]common here, and we get:
\[ \Rightarrow m(h) = \dfrac{{h(2 - h)}}{h}\]
Now, the common terms from the numerator and denominator get cancelled. Here, \[h\] gets cancelled from both numerator and denominator, and we get:
\[ \Rightarrow m(h) = (2 - h)\]
Therefore, we get the slope as \[(2 - h)\].
If we calculate by taking limit, then \[\mathop {\lim }\limits_{h \to 0} \,m(h) = \mathop {\lim }\limits_{h \to 0} \,2 - h\]. We get our answer as \[2\]. This is the coefficient of the tangent line to \[f(x)\] at the point \[2\].
Note: While plotting a graph, when we draw a line on that graph of curve, if the line intersects that curve at two or more than two points, then that line is a secant line, as we can see in the following graph, the blue line is a secant to the curve because it is intersecting the curve twice at “A” and “B”
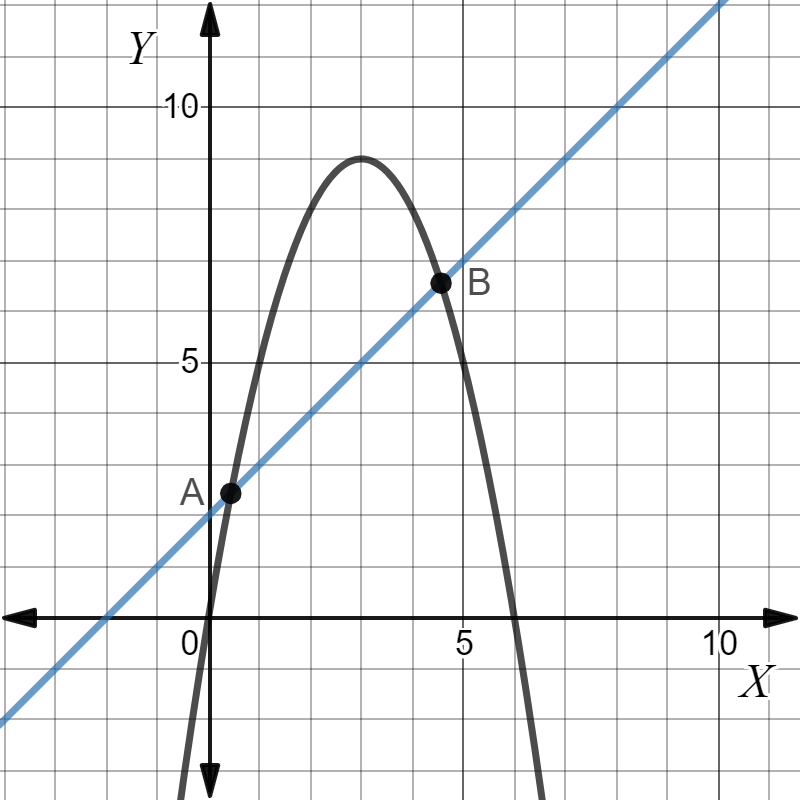
Formula used: \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
Complete step by step answer:
Slope also means gradient here.
According to this question, we have to find the slope by using the two points. Here, we will use the gradient formula to find the slope or gradient. The formula is:
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
In this formula, \[({x_1},{y_1})\,\,and\,\,({x_2},{y_2})\] are the points. So, according to the question, we get:
\[({x_1},{y_1}) = (2,f(2))\] and \[({x_2},{y_2}) = (2 + h,f(2 + h))\]
Now, we will put the values or points in the formula, and we get:
\[ \Rightarrow m(h) = \dfrac{{f(2 + h) - f(2)}}{{2 + h - 2}}\]
Now, we will substitute the values \[6x - {x^2}\] in the solving part, and we get:
\[ \Rightarrow m(h) = \dfrac{{(6 - (2 + h))(2 + h) - (6 \times 2 - {2^2})}}{{2 + h - 2}}\]
Now, we will simplify the denominator, and we get:
\[ \Rightarrow m(h) = \dfrac{{(6 - (2 + h))(2 + h) - (6 \times 2 - {2^2})}}{h}\]
Now, we will simplify the numerator, and we get:
\[ \Rightarrow m(h) = \dfrac{{(4 - h)(2 + h) - (12 - 4)}}{h}\]
\[ \Rightarrow m(h) = \dfrac{{4(2 + h) - h(2 + h) - 8}}{h}\]
\[ \Rightarrow m(h) = \dfrac{{8 + 4h - 2h - {h^2} - 8}}{h}\]
\[ \Rightarrow m(h) = \dfrac{{2h - {h^2}}}{h}\]
Now, we will take \[h\]common here, and we get:
\[ \Rightarrow m(h) = \dfrac{{h(2 - h)}}{h}\]
Now, the common terms from the numerator and denominator get cancelled. Here, \[h\] gets cancelled from both numerator and denominator, and we get:
\[ \Rightarrow m(h) = (2 - h)\]
Therefore, we get the slope as \[(2 - h)\].
If we calculate by taking limit, then \[\mathop {\lim }\limits_{h \to 0} \,m(h) = \mathop {\lim }\limits_{h \to 0} \,2 - h\]. We get our answer as \[2\]. This is the coefficient of the tangent line to \[f(x)\] at the point \[2\].
Note: While plotting a graph, when we draw a line on that graph of curve, if the line intersects that curve at two or more than two points, then that line is a secant line, as we can see in the following graph, the blue line is a secant to the curve because it is intersecting the curve twice at “A” and “B”

Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




