Question

Find the slope of the line passing through the points:
(i) (-2, 3) and (8, -5)
(ii) (4, -3) and (6, -3)
(iii) (3, 2) and (3, -1)

Answer 1

Hint: We know that the slope of a line joining the two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is equal to the tangent of the angle made by the line with x-axis in anticlockwise direction by as follows:
\[slope=\tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
Complete step-by-step answer:
We will find the slope of a line passing through the following points as below:
(i) (-2, 3) and (8, -5)
We know that the slope of a line passing through the two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by,
\[slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]

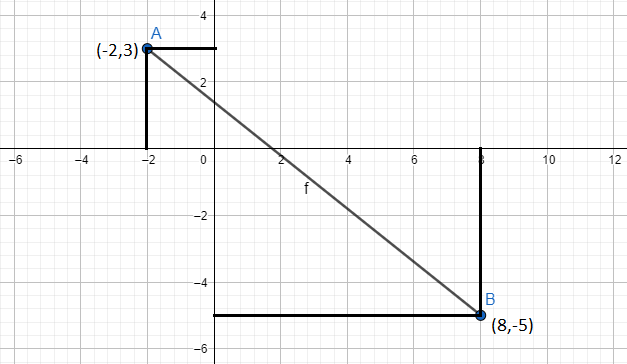
So we have \[{{x}_{1}}=-2,{{y}_{1}}=3,{{x}_{2}}=8,{{y}_{2}}=-5\]
\[\Rightarrow slope=\dfrac{-5-3}{8-(-2)}=\dfrac{-8}{8+2}=\dfrac{-8}{10}=\dfrac{-4}{5}\]
Hence the slope is equal to \[\left( \dfrac{-4}{5} \right)\].
(ii) (4, -3) and (6, -3)
We know that slope of a line passing through the points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by,
\[slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]

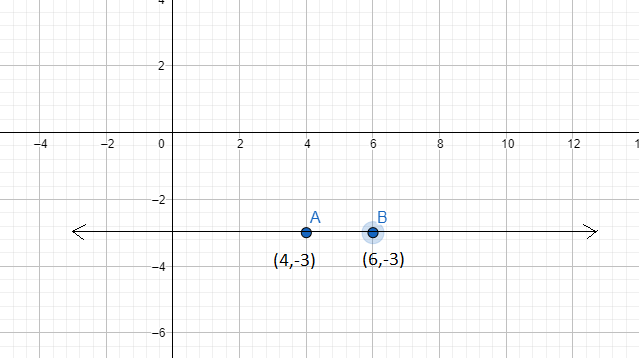
So we have \[{{x}_{1}}=4,{{y}_{1}}= -3,{{x}_{2}}=6,{{y}_{2}}=-3\]
\[\Rightarrow slope=\dfrac{-3-(-3)}{6-4}=\dfrac{0}{2}=0\]
Since we know that if the slope of a line is equal to 0 means the line is parallel to x-axis.
Hence, slope is equal to zero.
(iii) (3, 2) and (3, -1)
We know that the slope of a line passing through the points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by,
\[slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]

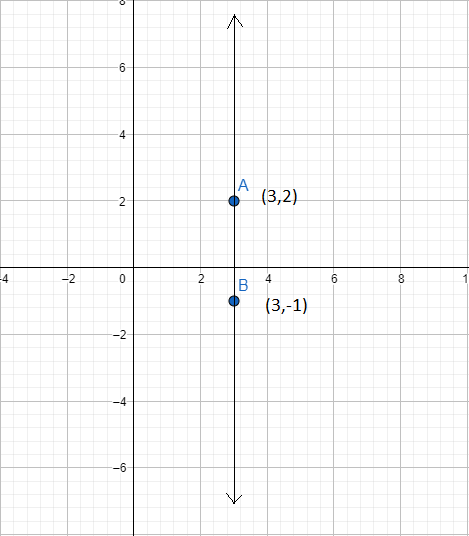
\[\Rightarrow slope=\dfrac{-1-2}{3-3}=\dfrac{-3}{0}=\infty (infinity)\]
Hence the slope is equal to infinity means the line is perpendicular to the x-axis.

Note: Substitute the value of \[{{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}}\] in the formula very carefully because if you misplace it order then you will get the incorrect answer. Also, remember that the slope of a line is also equal to the tangent value of the angle by the line and the x-axis in anticlockwise direction with respect to x-axis.