Question

Find the slope of the line and its intercept using the following equation of line: $y = 0.5x$

Answer 1

Hint:find the slope of a line when an equation of line is given in the question we must use the slope intercept form of a linear equation. In the slope intercept form of the line equation, the coefficient of $x$ is slope $m$ and the constant term with its proper sign is $y - {\text{intercept (c)}}$

Complete step by step solution:
Firstly we write the given equation$y = 0.5x{\text{ - - - - - - - - - (i)}}$
Simplifying the equation we have -
$y = \dfrac{1}{2}x$
As we know the equation of a line is given by-
$y\; = \;mx + c$
Where$\;m\; = \;{\text{slope}}\;{\text{of}}\;{\text{line}}$and $c = {\text{y -
intercept}}\;{\text{of}}\;{\text{line}}$
Comparing this standard equation with equation (i) we get slope –
$m = \dfrac{1}{2}\;{\text{and}}\;c = 0$
Here we get the desired result and the value of $c = 0$ shows that the line passes through the origin.

Note: Slope of a line can be understood, in layman terms, as rise over run in a Cartesian coordinate system. In this there are two axes namely $x - axis\;{\text{and}}\;y - axis $ more precisely; Slope of a line is the change in the values of $y$ with respect to the change in values of $x$. It is denoted as $m$ which is a debatable notation for it because it is not clear why it is represented with $m$

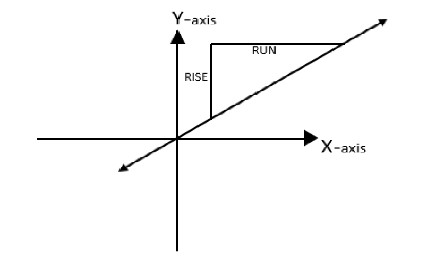
Here the slope will be the ratio of value of $y - axis\;{\text{and}}\;x - axis$ meaning it characterizes the direction of line. By the figure itself, we can see that while finding a slope when two point of a line are given we simply divide the difference of the $y$ coordinates of the 2 points by the difference of the $x$ coordinates of the two same points i.e.
Two points of a line a given as$({x_{1,}}{y_1})\;{\text{and}}\;({x_{2,}}{y_2})$then we calculate the slope as- $m\; = \;\dfrac{{({y_2} - {y_1})}}{{({x_2} - {x_1})}}$