Question

How do you find the slope of the curve \[f(x) = \sqrt {x - 1} \] at the point \[x = 5\]?

Answer 1

Hint: We need to find the slope of the curve \[f(x)\] at the given point \[x = a\]. But, here the value of independent value is given as \[x = 5\] and differentiate the function \[f(x) = \sqrt {x - 1} \] as \[f'(x)\] at the given point and plot a graph for the function and values.

Complete step by step solution:
Given,
The slope of a function \[f(x) = \sqrt {x - 1} \] at the point \[x = 5\].
To find a slope of curve,
By substitute point value into the function to art a graph,
To find curve at the point \[(5,2)\] is mention below the following,

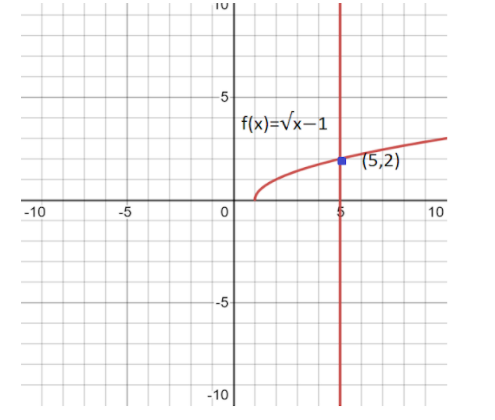
The slope of curve function \[f(x) = \sqrt {x - 1} \]……………..\[(1)\]
We have, the given Point at\[x = 5\],
By take out the square root as power of \[\dfrac{1}{2}\], we get
\[f(x) = {(x - 1)^{1/2}}\]
Differentiate the slope of function with respect to \[x\], then we get
\[f'(x) = \dfrac{1}{2}{(x - 1)^{\dfrac{1}{2} - 1}}\]
By simplify the power fraction value, we get
\[\]
To simplify, we get
\[f'(x) = \dfrac{1}{2}{(x - 1)^{ - \dfrac{1}{2}}}\]
By write the power\[ - \dfrac{1}{2}\] as fraction, we have
\[f'(x) = \dfrac{1}{{2{{(x - 1)}^{\dfrac{1}{2}}}}}\]……………\[(2)\]
By substitute the point value\[x = 5\] in the equation\[(2)\],
\[f'(5) = \dfrac{1}{{2{{(5 - 1)}^{\dfrac{1}{2}}}}}\]
By simplify the denominator value, we get
\[f'(5) = \dfrac{1}{{2{{(4)}^{\dfrac{1}{2}}}}}\]
Put the power value by take square root, we get
 \[f'(5) = \dfrac{1}{{2\sqrt 4 }} = \dfrac{1}{{2\sqrt {2 \times 2} }}\]
By remove the square root to simplify, we get
\[f'(5) = \dfrac{1}{{2 \times 2}} = \pm \dfrac{1}{4}\]
\[f'(5) = \pm \dfrac{1}{4}\]
Hence, the slope of the curve at the given value is \[ \pm \dfrac{1}{4}\].

Note: We need the slope of the curve function, \[f(x) = \sqrt {x - 1} \] at the point of independent variable \[x = 5\]. By substitute the given values into the function and plot a graph with respect to the function and the point. We need to remember the concept to solve the problems with different values.