Question

How do you find the slope of $\left( 3,5 \right)$ and $\left( 2,1 \right)$ ?

Answer 1

Hint: This problem can be solved easily by the slope-intercept form of a straight line, which states that if two points on a straight line are $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ then, the equation of the straight line would be
$\dfrac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}$

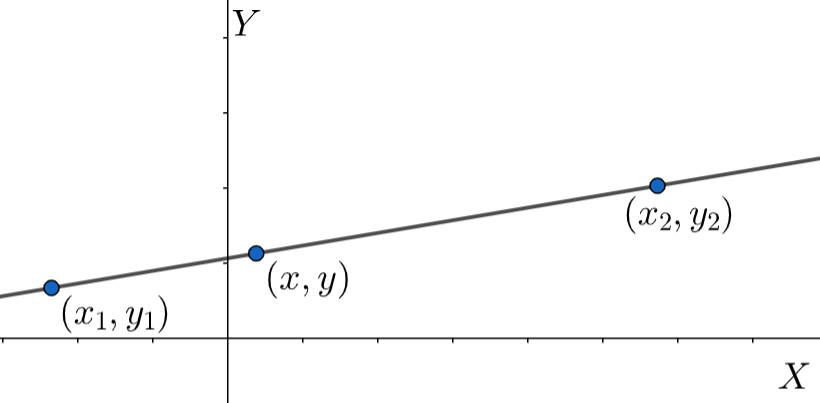
After putting the given points in this equation, we get the slope of the straight line.

Complete step-by-step answer:
For any straight line, if any two points on the line are known then, we can write the equation of the straight line as
$\dfrac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}....equation1$
This is called the two point form. Here, $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the two known points on the line and $\left( x,y \right)$ is any arbitrary point on the same line. In the given problem, the two points given are $\left( 3,5 \right)$ and $\left( 2,1 \right)$ . Therefore, let us assume
$\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,5 \right)$
$\left( {{x}_{2}},{{y}_{2}} \right)=\left( 2,1 \right)$
Putting these values in $equation1$ , we get,
$\Rightarrow \dfrac{y-5}{1-5}=\dfrac{x-3}{2-3}$
$\Rightarrow \dfrac{y-5}{-4}=\dfrac{x-3}{-1}$
Multiplying both sides by $\left( -4 \right)$ , we get,
$\begin{align}
  & \Rightarrow y-5=4\left( x-3 \right) \\
 & \Rightarrow y-5=4x-12 \\
\end{align}$
Adding $5$ on both sides of the equation, we get,
$\Rightarrow y-5=4x-12+5$
$\Rightarrow y=4x-7....equation2$
Comparing equation 2 with the slope-intercept form $y=mx+c$ , where $m$ is the slope of the line and $c$ is the y-intercept, we get,
$m=4$ and $c=-7$
Therefore, we can conclude that the slope of the line joining $\left( 3,5 \right)$ and $\left( 2,1 \right)$ is $4$ .

Note: The common mistake made by most of the students is that while putting the values of ${{x}_{1}}$ , ${{x}_{2}}$ and so on, they interchange the values. This mistake can lead to negative answers or even completely wrong answers at times. An alternate method to solve this problem is by taking the slope-intercept form of a straight line $y=mx+c$ , putting the points in the equation one by one, and finally subtract the two equations formed to get the value of slope.