Question

How do you find the slope and y intercept of $y=2x+4$?

Answer 1

Hint: Problems on coordinate geometry can be easily solved by comparing the given equation to the general equation of the same type. In this case the given equation is an equation of a straight line. So, we compare $y=2x+4$ with the general equation of a straight line, i.e., $y=mx+c$ which is the slope-intercept form of a straight line.

Complete step-by-step answer:
The given equation we have is
$y=2x+4....\text{equation}1$
As this is an equation of a simple straight line and it is already presented in the slope-intercept form, we will compare it with the general equation of a straight line in slope-intercept form.
$y=mx+c....\text{equation}2$
Here, the $m$ represents the slope (tangent of the angle made by the line with $x$ -axis) of the straight line. Also, if we put $x=0$ in the equation we see that $y=c$ . Hence, $c$ is the $y$ intercept of the line.
Now, comparing $\text{equation}1$ and $\text{equation2}$, we get
$m=2$ and $c=4$
Therefore, we can conclude to the result that the given straight line has a\[\text{slope, }m=2\] and $y$ intercept, $c=4$.

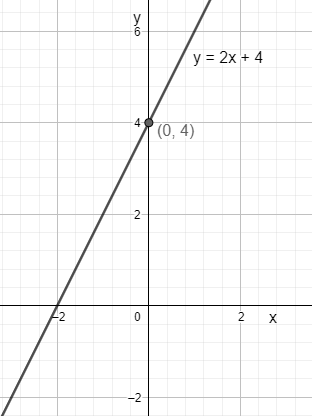
Note: Before comparing the straight-line equation with the general form, we must check whether the equation is in the slope and $y$ intercept form. Otherwise, we need to convert the given equation into the slope and $y$ intercept form and then compare it with $y=mx+c$. Also, this problem can be solved with the help of another method i.e., Graphical method. First, we have to find out any two points which satisfies the equation and then plot it on graph paper. Connecting the two points we get the line on the graph paper. Now, we will be able to find the slope of the line by measuring the angle with a protractor and the $y$ intercept by measuring the length of the $y\text{-axis}$ up to the point it is intercepted by the line.