Question

How can you find the slope and intercept of \[\dfrac{3}{4}x - y = 4\]?

Answer 1

Hint: Since we need to find the slope and intercept so we need to convert the equation into slope-intercept form by solving \[y\]and any linear equation has the form of \[y = mx + c\] where \[m\] stands as slope which can be found by finding two distinct points and \[c\] is the \[y\] intercept where graph hits \[y\] axis.

Formula used:
Since slope \[m\] depicts how steep the line is with respect to horizontal. So if in the line two points found are \[({x_1},{y_1})\] and \[({x_2},{y_2})\] so slope comes out to be
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
The point where line crosses why \[y\] axis is the \[y\] intercept \[c\]

Complete step by step solution:
As the given equation is \[\dfrac{3}{4}x - y = 4\]
Since we know that \[y = mx + c\] is the slope intercept form of a line where \[m\] is equal to slope and \[c\]is the \[y\] intercept
So here we will subtract \[\dfrac{3}{4}x\] from each side of equation
\[
   \Rightarrow \dfrac{3}{4}x - \dfrac{3}{4}x - y = - \dfrac{3}{4}x + 4 \\
   \Rightarrow - y = - \dfrac{3}{4}x + 4 \\
 \]
Now after dividing \[ - 1\] from both sides we will get
\[y = \dfrac{3}{4}x + ( - 4)\]
So we will find that slope is \[m = \dfrac{3}{4}\] and \[c\] be the \[y\] intercept is \[ - 4\]
Now we will plot the graph

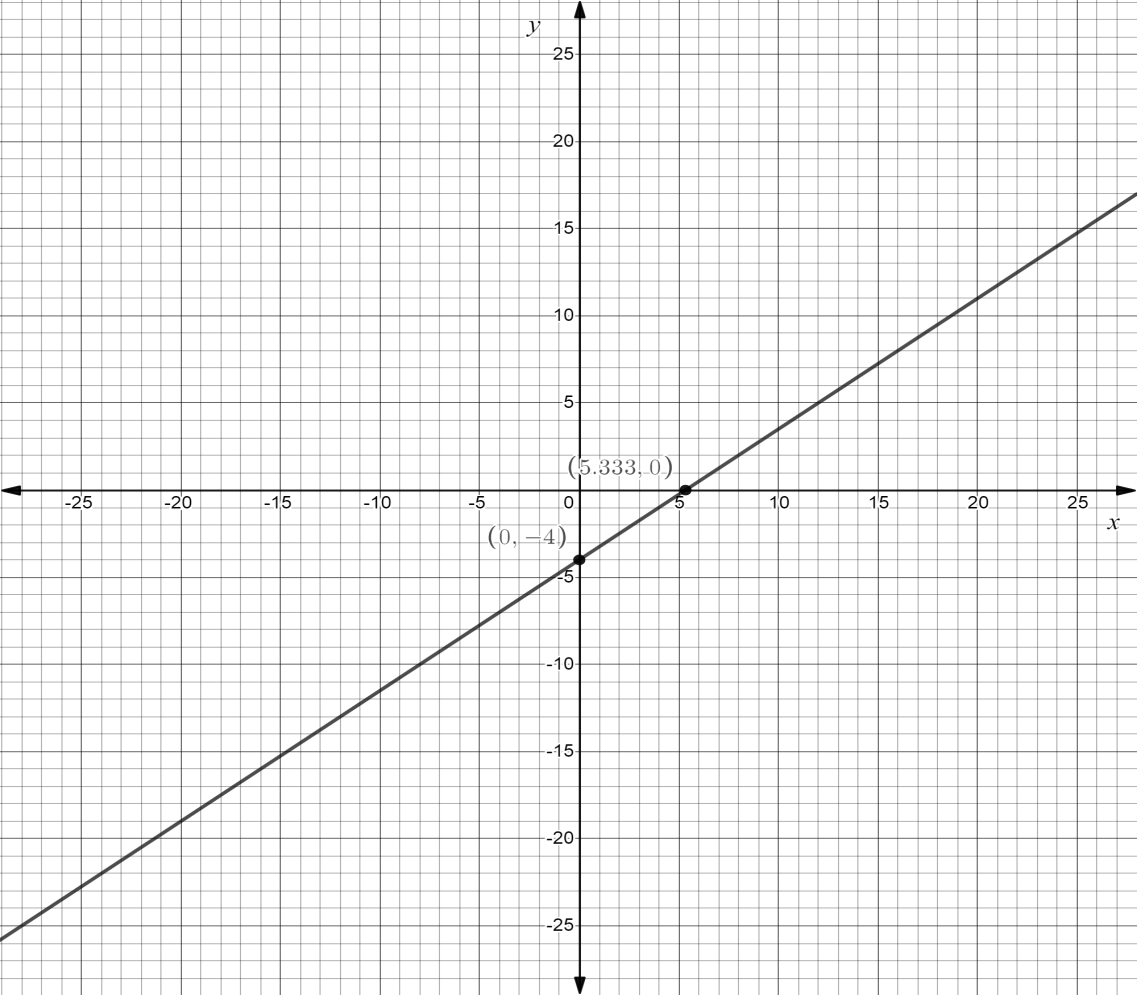
Additional Information:
Keep in mind that slopes can be negative or positive. Here y will tell how far a line goes, x tells us how far along it goes, m tells about the slope and c is the intercept where the lines crosses y axis

Note: While solving the above equation we need to convert the equation given in the slope intercept form and later on after finding the value of \[m\] and \[c\] then pick a point on line and check if it satisfies the equation by plugging it in. So \[x\] intercept is \[\left( {\dfrac{{16}}{3},0} \right)\] and \[y\] intercept is \[(0, - 4)\] which mean line cuts \[y\] axis at \[ - 4\]