Question

How do you find the slope and intercept of \[4x=y+8\]?

Answer 1

Hint: From the question, we have been asked to find the slope and intercept of \[4x=y+8\] We can find the slope and intercept of the given equation by converting the given equation into \[y=mx+b\] form.

Complete step-by-step solution:
In this \[y=mx+b\] form of the equation \[b\] is your \[y\]-intercept and \[m\] is your slope.
Now, as of process, we have to convert the given equation into \[y=mx+b\] form.
From the question, we have been given that \[4x=y+8\]
Now, take away \[8\] from both sides of the given equation.
By taking away \[8\] from both sides of the equation, we get the below equation,
\[4x-8=y+8-8\]
\[\Rightarrow 4x-8=y\]
Now, rearrange the equation into the form of \[y=mx+b\].
By rearranging the obtained equation into \[y=mx+b\] form, we get the below equation \[y=4x-8\]
Now, we can clearly observe that the equation is in the form of \[y=mx+b\].
Now, compare the coefficients of both the equations to get the slope of the equation.
By comparing the coefficients, we get the slope of the equation \[=m=4\].

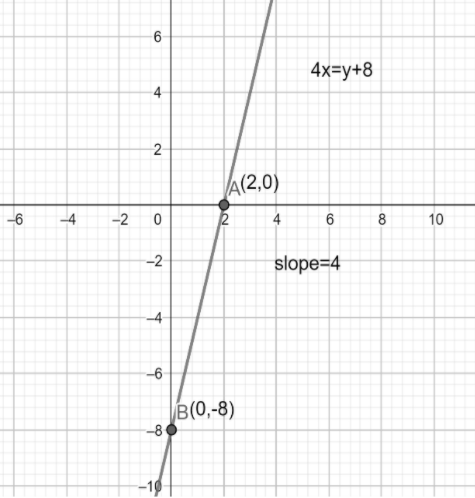
Now, we have to find the intercept.
First of all, let us find the \[y\] intercept.
\[y=4x-8\]
When the line crosses the \[y\] axis, \[x\] is at zero, so we can use \[x=0\] to find \[y\] intercept.
\[\begin{align}
  & y=4\left( 0 \right)-8 \\
 & \Rightarrow y=-8 \\
\end{align}\]
Therefore, we got the \[y\] intercept.
Now, we have to find \[x\] intercept.
\[y=4x-8\]
When the line crosses the \[x\] axis, \[y\] is zero. So, we can make \[y=0\] in our equation.
\[\begin{align}
  & 0=4x-8 \\
 & 8=4x \\
 & x=2 \\
\end{align}\]
Therefore, we got the \[x\] intercept.

Note: We should be well aware of the concept of slope and intercept. We should be very careful while converting the given equation into slope-intercept form. Also, we should be very careful while doing the calculation of finding the intercepts. Also, we should be careful while finding the slope of the given equation. There is another way to find the slope of an equation joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ . For this question $4x=y+8$ it will be $\left( 0,-8 \right)$ and $\left( 2,0 \right)$ given as $m=\dfrac{0-\left( -8 \right)}{2-0}=4$ .