Question

Find the slant height of a frustum cone whose top radius is 12 m and bottom radius is 10 m. The height of the cone is 13 m.
A. 13.15 m
B. 12.15 m
C. 10.15 m
D. 14.25 m

Answer 1

Hint: First draw the diagram on the base of data provided in the question. After that find the difference between the top radius and the bottom radius. Then, use the Pythagoras theorem to find the slant height of the frustum by using the height and the difference of the radius of the frustum and simplify.

Complete step-by-step solution:
The diagram on basis of data provided in the question is,

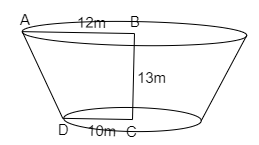
Draw a perpendicular from D on AB which meets at E.

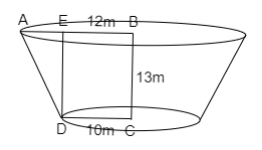
Let the height of the frustum be AD.
As, DE is the distance from the top of the frustum to the bottom, which is the height of the frustum. So,
$ \Rightarrow DE = 13$m……………...….. (1)
Now find the length of AE.
As DE is perpendicular from D on AB. Then the length of BE is equal to the length of DC. So,
$ \Rightarrow BE = 10$m
Now, the length of AE is the difference between the length of AB and BE. So,
$ \Rightarrow AE = AB - BE$
Substitute the values,
$ \Rightarrow AE = 12 - 10$
Subtract the terms on the right side,
$ \Rightarrow AE = 2$m…………..….. (2)
Now, in $\Delta ADE$, apply Pythagoras Theorem,
$A{D^2} = D{E^2} + A{E^2}$
Substitute the values of DE and AE from equation (1) and (2),
$ \Rightarrow A{D^2} = {13^2} + {2^2}$
Square the terms on the right side,
$ \Rightarrow A{D^2} = 169 + 4$
Add the terms,
$ \Rightarrow A{D^2} = 173$
Take the square root on both sides,
$ \Rightarrow AD = \sqrt {173} $
Simplify the terms,
$\therefore AD = 13.15$m
Hence, the height of the frustum is 13.15 m.

Option A is the correct option.

Note: The students might make mistakes by not finding the difference of radius and then applying Pythagoras Theorem. It may lead to a lengthy calculation or even a wrong answer.
The slant height of a frustum of a right circular cone is the line segment joining the extreme point of two parallel radii, drawn in the same direction, of the two circular bases.