Question

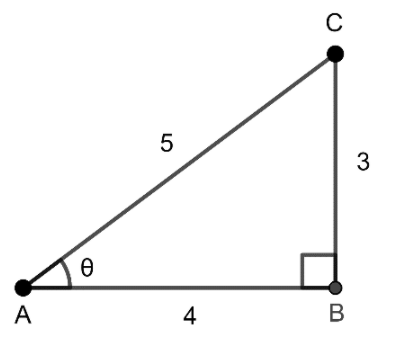
Find the six trigonometric ratios of the angle \[\theta \] in the right triangle $ABC$, as shown at right.

Answer 1

Hint: Here in this right-angled triangle the opposite side of the angle $\theta $ is $CB$ and the adjacent side of the angle is $AB$. And the Hypotenuse in this triangle is $AC$. Use this information to find the value of trigonometric functions.

Complete step by step solution:
We know that there are six trigonometric ratios namely sine, cosine, tangent, cosecant, secant and cotangent. And these six trigonometric ratios are usually abbreviated as sin, cos, tan, csc, sec, cot. We are calling them as ratios as they can be expressed in terms of the sides of a right-angled triangle for a specific angle $\theta $.
Recall that the side opposite to the right angle in a right triangle is called the hypotenuse of the triangle. We also know that the side opposite to an angle other than right angle in a right triangle is called as the opposite side of the angle. And also, the side other than these two sides is known as the adjacent side of the angle.
From the definitions of the trigonometric ratios, we know that $\sin x = \dfrac{{opposite}}{{hypotenuse}}$, $\cos x = \dfrac{{adjacent}}{{hypotenuse}}$, $\tan x = \dfrac{{opposite}}{{adjacent}} = \dfrac{{\sin x}}{{\cos x}}$. The remaining three ratios can be written as $\sec x = \dfrac{1}{{\cos x}}$, $\csc x = \dfrac{1}{{\sin x}}$ and $\cot x = \dfrac{1}{{\tan x}}$. We will use these definitions to find the required trigonometric ratios.
In the right triangle given, we are asked to find the trigonometric ratios of the angle $\theta $. Observe that the hypotenuse is $AC = 5$. And the opposite and adjacent sides to the angle $\theta $ are $CB = 3$ and $AB = 4$.
Now from definitions we get $\sin \theta = \dfrac{{opposite}}{{hypotenuse}} = \dfrac{{CB}}{{AC}}$.
$ \Rightarrow \sin \theta = \dfrac{3}{5}$
Also, $\cos \theta = \dfrac{{adjacent}}{{hypotenuse}} = \dfrac{{AB}}{{AC}}$ $ \Rightarrow \cos \theta = \dfrac{4}{5}$
We can see that $\tan \theta = \dfrac{{opposite}}{{adjacent}} = \dfrac{{CB}}{{AB}}$ $ \Rightarrow \tan \theta = \dfrac{3}{4}$.
Similarly, we get $\sec \theta = \dfrac{1}{{\cos \theta }} = \dfrac{5}{4}$
$\csc \theta = \dfrac{1}{{\sin \theta }} = \dfrac{5}{3}$ and $\cot \theta = \dfrac{1}{{\tan \theta }} = \dfrac{4}{3}$.
Hence the six trigonometric ratios of the angle $\theta $ are $\sin \theta = \dfrac{3}{5}$, $\cos \theta = \dfrac{4}{5}$, $\tan \theta = \dfrac{3}{4}$, $\csc \theta = \dfrac{5}{3}$, $\sec \theta = \dfrac{5}{4}$ and $\cot \theta = \dfrac{4}{3}$.

Note:
Many of them get confused with the opposite and adjacent sides of a given angle from a right-angled triangle. Always remember that the side opposite to the angle, that is the side which does not contain the angle is the opposite angle. And so, the remaining another leg is the adjacent side.