
How do you find the roots of ${x^3} + {x^2} - 5x + 3 = 0$?
Answer
555.3k+ views
Hint: Given a polynomial and the zeros of the polynomial are determined by finding the values of $x$ for which the polynomial is equal to zero. Then we will apply the rational root theorem which states that the rational root is of the form $r = \pm \dfrac{p}{q}$ where the denominator must divide by the leading coefficient and the numerator is divided by the constant. Then, the other factors are computed by a long division method. Then, factorize further the factors thus obtained by splitting the middle term.
Complete step-by-step answer:
Here in the polynomial, $q = 1$ and $p = 3$. First, we will find the factors of the trailing constant.
$p = 1,3$
Therefore, the possible rational roots of the polynomial are $ \pm \dfrac{1}{1}, \pm \dfrac{3}{1}$
Now we will substitute the value of roots one by one into the polynomial to check for which value the polynomial is zero.
By substituting $x = 1$ into the polynomial.
$ \Rightarrow {\left( 1 \right)^3} + {\left( 1 \right)^2} - 5\left( 1 \right) + 3$
On simplifying the expression, we get:
$ \Rightarrow 1 + 1 - 5 + 3 = 0$
Thus, $f\left( x \right) = 0$ at $x = 1$ which means $\left( {x - 1} \right)$ is a factor of the polynomial.
We will find other factors of the polynomial by dividing the polynomial by the factor $\left( {x - 1} \right)$ using the long division method.
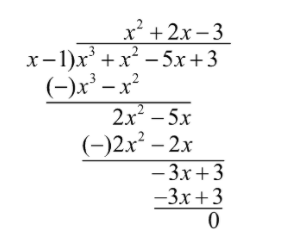
Thus, the factors of the polynomial are $\left( {x - 1} \right)\left( {{x^2} + 2x - 3} \right)$
Now, we will factorize the factor ${x^2} + 2x - 3$ by splitting the middle term whose sum is $2$ and product is $ - 3$.
$ \Rightarrow {x^2} + 3x - x - 3$
\[ \Rightarrow x\left( {x + 3} \right) - 1\left( {x + 3} \right)\]
\[ \Rightarrow \left( {x - 1} \right)\left( {x + 3} \right)\]
Hence, the factors of the polynomial are \[\left( {x - 1} \right)\left( {x - 1} \right)\left( {x + 3} \right)\].
Note:
In such types of questions students mainly don't get an approach on how to solve it. In such types of questions students mainly forget to apply the rational root theorem by which factorizes the whole expression. Sometimes we have to factor out a number from an expression then the expression forms in a way so that it can be factorized and identity can be applied. In such types of questions, to factor, the polynomial synthetic division can also be used instead of the long division process.
Complete step-by-step answer:
Here in the polynomial, $q = 1$ and $p = 3$. First, we will find the factors of the trailing constant.
$p = 1,3$
Therefore, the possible rational roots of the polynomial are $ \pm \dfrac{1}{1}, \pm \dfrac{3}{1}$
Now we will substitute the value of roots one by one into the polynomial to check for which value the polynomial is zero.
By substituting $x = 1$ into the polynomial.
$ \Rightarrow {\left( 1 \right)^3} + {\left( 1 \right)^2} - 5\left( 1 \right) + 3$
On simplifying the expression, we get:
$ \Rightarrow 1 + 1 - 5 + 3 = 0$
Thus, $f\left( x \right) = 0$ at $x = 1$ which means $\left( {x - 1} \right)$ is a factor of the polynomial.
We will find other factors of the polynomial by dividing the polynomial by the factor $\left( {x - 1} \right)$ using the long division method.
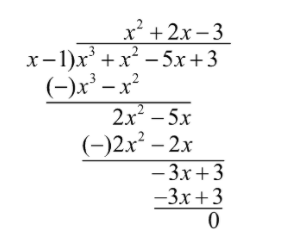
Thus, the factors of the polynomial are $\left( {x - 1} \right)\left( {{x^2} + 2x - 3} \right)$
Now, we will factorize the factor ${x^2} + 2x - 3$ by splitting the middle term whose sum is $2$ and product is $ - 3$.
$ \Rightarrow {x^2} + 3x - x - 3$
\[ \Rightarrow x\left( {x + 3} \right) - 1\left( {x + 3} \right)\]
\[ \Rightarrow \left( {x - 1} \right)\left( {x + 3} \right)\]
Hence, the factors of the polynomial are \[\left( {x - 1} \right)\left( {x - 1} \right)\left( {x + 3} \right)\].
Note:
In such types of questions students mainly don't get an approach on how to solve it. In such types of questions students mainly forget to apply the rational root theorem by which factorizes the whole expression. Sometimes we have to factor out a number from an expression then the expression forms in a way so that it can be factorized and identity can be applied. In such types of questions, to factor, the polynomial synthetic division can also be used instead of the long division process.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




