Question

How do you find the remaining side of a $30^\circ $ $ - 60^\circ $ $ - 90^\circ $ triangle if the longest side is 8?

Answer 1

Hint: In this question, we are given one of the sides of a triangle and the three angles of the triangle. As one of the angles is equal to 90 degrees so trigonometric functions can be used for solving this question. Trigonometric functions tell us the link between two sides of the right-angled triangle and one of its angles. So, by using a trigonometric function that tells us the link between one unknown side, the known side and one of the angles, we can find the value of the unknown sides.

Complete step-by-step answer:
We are given a $30^\circ $ $ - 60^\circ $ $ - 90^\circ $ triangle and the longest side of this triangle is 8, that is, the length of the hypotenuse is equal to 8. Let the triangle be represented as –

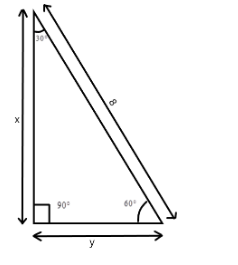
In this triangle, “y” is the base (B), “x” is the perpendicular (P) and 8 is the hypotenuse (H).
We know the sine of an angle is equal to the ratio of the perpendicular and the hypotenuse of the right-angled triangle –
$
  \sin \theta = \dfrac{P}{H} \\
   \Rightarrow \sin 60^\circ = \dfrac{x}{8} \\
   \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{x}{8} \\
   \Rightarrow x = 4\sqrt 3 \;
 $
And cosine function is equal to the ratio of the base and the hypotenuse of the right-angled triangle –
$
  \cos \theta = \dfrac{B}{H} \\
   \Rightarrow \cos 60^\circ = \dfrac{y}{8} \\
   \Rightarrow \dfrac{1}{2} = \dfrac{y}{8} \;
   \Rightarrow y = 4 \;
 $
Hence the remaining sides of a $30^\circ $ $ - 60^\circ $ $ - 90^\circ $ triangle if the longest side is 8 are $4\sqrt 3 $ and $4$ .

Note: There is a theorem named Pythagoras theorem that tells us the link between the three sides of a right-angled triangle. According to the Pythagoras theorem –
${H^2} = {B^2} + {P^2}$
From this equation, we see that hypotenuse is greater than both the perpendicular and the base, that’s why it is the longest side of the right-angled triangle.