Question

Find the relation between ${{t}_{1}}$ and ${{t}_{2}}$ , where the normal at ${{t}_{1}}$ to the parabola ${{y}^{2}}=4ax$ meets the parabola ${{y}^{2}}=4ax$ again at ${{t}_{2}}$ .

Answer 1

Hint: The given problem is related to the equation of normal to parabola in parametric form. The general equation of the normal to the parabola at a point \[\left( a{{t}^{2}},2at \right)\] is given by \[y=-tx+2at+a{{t}^{3}}\] , where \[t\] is a parameter. Find the equation of normal at ${{t}_{1}}$ , then substitute the point ${{t}_{2}}$ in the equation of the normal. On simplifying the equation, we will get the relation between ${{t}_{1}}$ and ${{t}_{2}}$ .

Complete step-by-step answer:
We are given the equation of the parabola as \[{{y}^{2}}=4ax\] .
Now, we will consider two points on the parabola given by \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] , where \[{{t}_{1}}\] , and \[{{t}_{2}}\] are parameters.

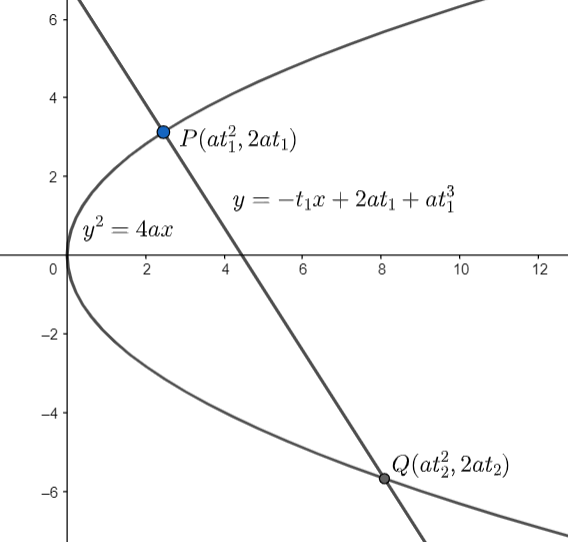
Now, we need to find the equation of normal at \[P\].
We know, the general equation of the normal to the parabola at a point \[\left( a{{t}^{2}},2at \right)\] is given by \[y=-tx+2at+a{{t}^{3}}\] , where \[t\] is a parameter.
So, the normal to the parabola at the point \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] will be given is given by substituting \[{{t}_{1}}\] in place of \[t\] in the general equation of the normal.
On substituting \[{{t}_{1}}\] in place of \[t\] in the general equation of the normal, we get \[y=-{{t}_{1}}x+2a{{t}_{1}}+at_{1}^{3}....\left( i \right)\] .
Now, we are given that the normal at \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] intersects the parabola at \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] . So, \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] should lie on the normal and hence, will satisfy the equation of the normal at \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] . So, we will substitute $x=at_{2}^{2}$ and $y=2a{{t}_{2}}$ in equation (i). On substituting $x=at_{2}^{2}$ and $y=2a{{t}_{2}}$ in equation (i), we get:
\[2a{{t}_{2}}=-{{t}_{1}}\left( at_{2}^{2} \right)+2a{{t}_{1}}+at_{1}^{3}\]
$\Rightarrow 2a{{t}_{2}}-2a{{t}_{1}}=-at_{2}^{2}{{t}_{1}}+at_{1}^{3}$
$\Rightarrow 2a\left( {{t}_{2}}-{{t}_{1}} \right)=-a{{t}_{1}}\left( t_{2}^{2}-t_{1}^{2} \right)$
 $\Rightarrow 2\left( {{t}_{2}}-{{t}_{1}} \right)=-{{t}_{1}}\left( t_{2}^{2}-t_{1}^{2} \right)$
Now, we know, we can write $t_{2}^{2}-t_{1}^{2}$ as $\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)$ . So, we get:
$\Rightarrow 2\left( {{t}_{2}}-{{t}_{1}} \right)=-{{t}_{1}}\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)$
$\Rightarrow 2=-{{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)$
$\Rightarrow \dfrac{-2}{{{t}_{1}}}={{t}_{1}}+{{t}_{2}}$
 $\Rightarrow \dfrac{-2}{{{t}_{1}}}-{{t}_{1}}={{t}_{2}}$
Hence, the relation between ${{t}_{1}}$ and ${{t}_{2}}$ , where the normal at ${{t}_{1}}$ to the parabola ${{y}^{2}}=4ax$ meets the parabola ${{y}^{2}}=4ax$ again at ${{t}_{2}}$ is given as ${{t}_{2}}=\dfrac{-2}{{{t}_{1}}}-{{t}_{1}}$ .

Note: While simplifying the equations, please make sure that sign mistakes do not occur. These mistakes are very common and can confuse while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken.