Question

Find the reference angles corresponding to given angles. It may help if you sketch $ \theta $ in the standard position, $ \dfrac{{31\pi }}{9} = \dfrac{{a\pi }}{9} $ Find a.

Answer 1

Hint: Find the angle with which the given angle makes with the nearest $ x - axis $ , which is the reference angle.
We first, make the angle in the found quadrants to find the reference of the given angle. Then, we find the number of revolutions in terms of $ \pi $ from one $ x - axis $ to another $ x - axis $ and then we can easily find the reference angle.
So, the given angle has made 3 revolutions in terms of $ \pi $ , So we can proceed finding the reference angle of the given angles as we have sketched it above.

Complete step by step solution:
Given that
 $ \dfrac{{31\pi }}{9} $ is the corresponding angle, we have to find the reference angle for this.
To find the angle, we find the revolutions in terms of $ \pi $ and add the remaining left angle, which will become the reference angle.

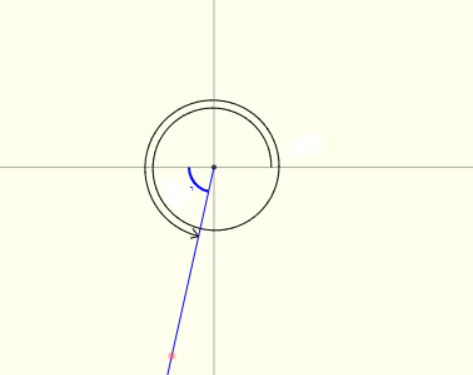
 $ \dfrac{{31\pi }}{9} $ has made 3 revolutions in terms of $ \pi $ , so it can be written as

 $ \dfrac{{31\pi }}{9} = 3\pi + \dfrac{{4\pi }}{9} $
Hence, we have found the reference angle which is $ \dfrac{{4\pi }}{9} $ .
In the question, we have been given that the reference of the given angle is equal to
 $ \dfrac{{31\pi }}{9} = \dfrac{{a\pi }}{9} $
Now when we compare and equate the obtained reference value, we will get the value of a.
  $ \dfrac{{4\pi }}{9} = \dfrac{{a\pi }}{9} $

Hence, we have got the value of a which is 4.

Note: We have to always remember that reference angles are measured from the nearest $ x - axis $ (it can be before the given angle or after the given angle) as a base to measure the reference and not the $ y - axis $ to measure the reference angle.